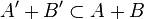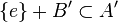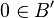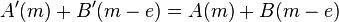Dyson's transform

Dyson's transform is a fundamental technique in additive number theory.^[1] It was developed by Freeman Dyson as part of his proof of Mann's theorem^[2]^:17, is used to prove such fundamental results of Additive Number Theory as the Cauchy-Davenport theorem,^[1] and was used by Olivier Ramaré in his work on the Goldbach conjecture that proved that every even integer is the sum of at most 6 primes.^[3]^:700–701 The term Dyson's transform for this technique is used by Ramaré.^[3]^:700–701 Halberstam and Roth call it the τ-transformation.^[2]^:58

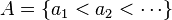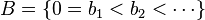This formulation of the transform is from Ramaré.^[3]^:700–701 Let A be a sequence of natural numbers, and x be any real number. Write A(x) for the number of elements of A which lie in [1, x]. Suppose $A= \{a_1<a_2< \cdots\}$ and $B= \{0=b_1<b_2<\cdots\}$ are two sequences of natural numbers. We write A + B for the sumset, that is, the set of all elements a + b where a is in A and b is in B; and similarly A − B for the set of differences a − b. 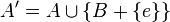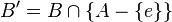For any element e in A, Dyson's transform consists in forming the sequences $A'= A \cup \{B + \{e\}\}$ and $\,B'= B \cap \{A - \{e\}\}$ . The transformed sequences have the properties:

$A' + B' \subset A + B$
$\{e\} + B' \subset A'$
$0 \in B'$
$A'(m)+ B'(m-e) = A(m) + B(m-e) \$

References

1 2 Additive Number Theory: Inverse Problems and the Geometry of Sumsets By Melvyn Bernard Nathanson, Springer, Aug 22, 1996, ISBN 0-387-94655-1, http://books.google.com/books?id=PqlQjNhjkKUC&dq=%22e-transform%22&source=gbs_navlinks_s, p. 42
1 2 Halberstam, H.; Roth, K. F. (1983). Sequences (revised ed.). Berlin: Springer-Verlag. ISBN 978-0-387-90801-4.
1 2 3 O. Ramaré (1995). "On šnirel'man's constant". Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 22 (4): 645–706. Retrieved 2009-03-13.

This article is issued from Wikipedia - version of the Tuesday, December 11, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.