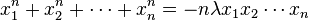Dwork family

In algebraic geometry, a Dwork family is a one-parameter family of hypersurfaces depending on an integer n, studied by Bernard Dwork. Originally considered by Dwork in the context of local zeta-functions, such families have been shown to have relationships with mirror symmetry and extensions of the modularity theorem.^[1]

Definition

The Dwork family is

x_1^n + x_2^n +\cdots +x_n^n = -n\lambda x_1x_2\cdots x_n \,

References

Katz, Nicholas M. (2009), "Another look at the Dwork family", Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. II (PDF), Progr. Math. 270, Boston, MA: Birkhäuser Boston, pp. 89–126, MR 2641188

↑ http://www.ams.org/journals/bull/2007-44-04/S0273-0979-07-01178-0/S0273-0979-07-01178-0.pdf, p. 545.

This article is issued from Wikipedia - version of the Saturday, April 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.