Dvoretzky's theorem

In mathematics, in the theory of Banach spaces, Dvoretzky's theorem is an important structural theorem proved by Aryeh Dvoretzky in the early 1960s.[1] It answered a question of Alexander Grothendieck. A new proof found by Vitali Milman in the 1970s[2] was one of the starting points for the development of asymptotic geometric analysis (also called asymptotic functional analysis or the local theory of Banach spaces).[3]

Original formulation

For every natural number k ∈ N and every ε > 0 there exists N(k, ε) ∈ N such that if (X,  ‖.‖) is a Banach space of dimension N(k, ε), there exist a subspace E ⊂ X of dimension k and a positive quadratic form Q on E such that the corresponding Euclidean norm

| \cdot | = \sqrt{Q(\cdot)}

on E satisfies:

|x| \leq \|x\| \leq (1+\epsilon)|x| \quad \text{for every} \quad x \in E.

Further development

In 1971, Vitali Milman gave a new proof of Dvoretzky's theorem, making use of the concentration of measure on the sphere to show that a random k-dimensional subspace satisfies the above inequality with probability very close to 1. The proof gives the sharp dependence on k:

N(k,\epsilon)\leq\exp(C(\epsilon)k).

Equivalently, for every Banach space (X,  ‖.‖) of dimension N, there exists a subspace E ⊂ X of dimension k ≥ c(ε) log N and a Euclidean norm |.| on E such that the inequality above holds.

More precisely, let Sn − 1 denote the unit sphere with respect to some Euclidean structure Q, and let σ be the invariant probability measure on Sn − 1. Then:

k = \dim E \geq c(\epsilon) \, \left(\frac{\int_{S^{n-1}} \| \xi \| \, d\sigma(\xi)}{\max_{\xi \in S^{n-1}} \| \xi \|}\right)^2 \, N.
c_1 \sqrt{\frac{\log N}{N}}.

Here c1 is a universal constant. The best possible k is denoted k*(X) and called the Dvoretzky dimension of X.

The dependence on ε was studied by Yehoram Gordon,[4][5] who showed that k*(X) ≥ c2 ε2 log N. Another proof of this result was given by Gideon Schechtman.[6]

Noga Alon and Vitali Milman showed that the logarithmic bound on the dimension of the subspace in Dvoretzky's theorem can be significantly improved, if one is willing to accept a subspace that is close either to a Euclidean space or to a Chebyshev space. Specifically, for some constant c, every n-dimensional space has a subspace of dimension k ≥ exp(c√(log N)) that is close either to ℓk
2 or to ℓk
∞.[7]

Important related results were proved by Tadeusz Figiel, Joram Lindenstrauss and Milman.[8]

References

  1. ↑ Dvoretzky, A. (1961). "Some results on convex bodies and Banach spaces". Proc. Internat. Sympos. Linear Spaces (Jerusalem, 1960). Jerusalem: Jerusalem Academic Press. pp. 123–160.
  2. ↑ Milman, V. D. (1971). "A new proof of A. Dvoretzky's theorem on cross-sections of convex bodies". Funkcional. Anal. i Prilozhen. (in Russian) 5 (4): 28–37.
  3. ↑ Gowers, W. T. (2000). "The two cultures of mathematics". Mathematics: frontiers and perspectives. Providence, RI: Amer. Math. Soc. pp. 65–78. ISBN 0-8218-2070-2. The full significance of measure concentration was first realized by Vitali Milman in his revolutionary proof [Mil1971] of the theorem of Dvoretzky ... Dvoretzky's theorem, especially as proved by Milman, is a milestone in the local (that is, finite-dimensional) theory of Banach spaces. While I feel sorry for a mathematician who cannot see its intrinsic appeal, this appeal on its own does not explain the enormous influence that the proof has had, well beyond Banach space theory, as a result of planting the idea of measure concentration in the minds of many mathematicians. Huge numbers of papers have now been published exploiting this idea or giving new techniques for showing that it holds.
  4. ↑ Gordon, Y. (1985). "Some inequalities for Gaussian processes and applications". Israel J. Math. 50 (4): 265–289. doi:10.1007/bf02759761.
  5. ↑ Gordon, Y. (1988). "Gaussian processes and almost spherical sections of convex bodies". Annals of Probability 16 (1): 180–188. doi:10.1214/aop/1176991893.
  6. ↑ Schechtman, G. (1989). "A remark concerning the dependence on ε in Dvoretzky's theorem". Geometric aspects of functional analysis (1987–88). Lecture Notes in Math. 1376. Berlin: Springer. pp. 274–277. ISBN 0-387-51303-5.
  7. ↑ Alon, N.; Milman, V. D. (1983), "Embedding of 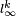\scriptstyle l^{k}_{\infty} in finite-dimensional Banach spaces", Israel Journal of Mathematics 45 (4): 265–280, doi:10.1007/BF02804012, MR 720303.
  8. ↑ Figiel, T.; Lindenstrauss, J.; Milman, V. D. (1976). "The dimension of almost spherical sections of convex bodies". Bull. Amer. Math. Soc. 82 (4): 575–578. doi:10.1090/s0002-9904-1976-14108-0., expanded in "The dimension of almost spherical sections of convex bodies", Acta Math. 139 (1977), 53–94.
This article is issued from Wikipedia - version of the Tuesday, December 02, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.