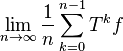Dunford–Schwartz theorem

In mathematics, particularly functional analysis, the Dunford–Schwartz theorem, named after Nelson Dunford and Jacob T. Schwartz states that the averages of powers of certain norm-bounded operators on L¹ converge in a suitable sense.^[1]

Statement of the theorem

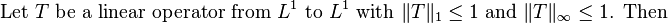
$\text{Let }T \text{ be a linear operator from }L^1 \text{ to }L^1 \text{ with }\|T\|_1\leq 1\text{ and }\|T\|_\infty\leq 1 \text{. Then}$

\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=0}^{n-1}T^kf

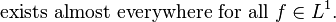
$\text{exists almost everywhere for all }f\in L^1\text{.}$

The statement is no longer true when the boundedness condition is relaxed to even 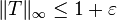$\|T\|_\infty\le 1+\varepsilon$ .^[2]

Notes

↑ Dunford, Nelson; Schwartz, J. T. (1956), "Convergence almost everywhere of operator averages", J. Rational Mech. Anal. 5: 129–178, MR 77090 .
↑ Friedman, N. (1966), "On the Dunford–Schwartz theorem", Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 5 (3): 226–231, doi:10.1007/BF00533059, MR 220900 .

This article is issued from Wikipedia - version of the Thursday, April 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.