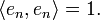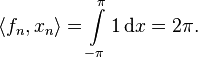Dunford–Pettis property

In functional analysis, the Dunford–Pettis property, named after Nelson Dunford and B. J. Pettis, is a property of a Banach space stating that all weakly compact operators from this space into another Banach space are completely continuous. Many standard Banach spaces have this property, most notably, the space C(K) of continuous functions on a compact space and the space L¹(μ) of the Lebesgue integrable functions on a measure space. Alexander Grothendieck introduced the concept in the early 1950s (Grothendieck 1953), following the work of Dunford and Pettis, who developed earlier results of Shizuo Kakutani, Kōsaku Yosida, and several others. Important results were obtained more recently by Jean Bourgain. Nevertheless, the Dunford–Pettis property is not completely understood.

Definition

A Banach space X has the Dunford–Pettis property if every continuous weakly compact operator T: X → Y from X into another Banach space Y transforms weakly compact sets in X into norm-compact sets in Y (such operators are called completely continuous). An important equivalent definition is that for any weakly convergent sequences (x_n) of X and (f_n) of the dual space X^∗, converging (weakly) to x and f, the sequence f_n(x_n) converges to f(x).

Counterexamples

• The second definition may appear counterintuitive at first, but consider an orthonormal basis e_n of a separable Hilbert space H. Then e_n → 0 weakly, but for all n,

Thus separable Hilbert spaces cannot have the Dunford–Pettis property.

• Consider as another example the space L^p(−π,π) where 1<p<∞. The sequences x_n=e^inx in L^p and f_n=e^inx in L^q = (L^p)* both converge weakly to zero. But

• More generally, no infinite-dimensional reflexive Banach space may have the Dunford–Pettis property. In particular, a Hilbert space and more generally, Lp spaces with 1 < p < ∞ do not possess this property.

Examples

• If X is a compact Hausdorff space, then the Banach space C(X) of continuous functions with the uniform norm has the Dunford–Pettis property.

References

• Bourgain, Jean (1981), "On the Dunford–Pettis property", Proceedings of the American Mathematical Society 81 (2): 265–272, doi:10.2307/2044207, JSTOR 2044207 
• Grothendieck, Alexander (1953), "Sur les applications linéaires faiblement compactes d'espaces du type C(K)", Canadian J. Math. 5: 129–173, doi:10.4153/CJM-1953-017-4 
• JMF Castillo, SY Shaw (2001), "Dunford–Pettis property", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Lin, Pei-Kee (2004), Köthe-Bochner Function Spaces, Birkhäuser, ISBN 0-8176-3521-1, OCLC 226084233 
• Randrianantoanina, Narcisse (1997), "Some remarks on the Dunford-Pettis property" (PDF), Rocky Mountain Journal of Mathematics 27 (4)