du Val singularity

In algebraic geometry, a du Val singularity, also called simple surface singularity, Kleinian singularity, or rational double point, is an isolated singularity of a complex surface which is modeled on a double branched cover of the plane, with minimal resolution obtained by replacing the singular point with a tree of smooth rational curves, with intersection pattern dual to a Dynkin diagram of A-D-E singularity type. They are the canonical singularities (or, equivalently, rational Gorenstein singularities) in dimension 2. They were studied by Patrick du Val (1934a, 1934b, 1934c) and Felix Klein.

The du Val singularities also appear as quotients of C² by a finite subgroup of SL₂(C); equivalently, a finite subgroup of SU(2), which are known as binary polyhedral groups. The rings of invariant polynomials of these finite group actions were computed by Klein, and are essentially the coordinate rings of the singularities; this is a classic result in invariant theory.

Classification

du Val singularies are classified by the simply laced Dynkin diagrams, a form of ADE classification.

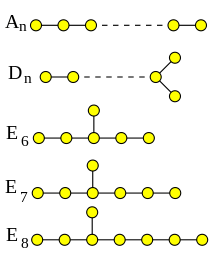
The possible du Val singularities are (up to analytic isomorphism):

• A_n:
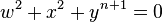
• D_n:
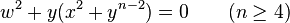
• E₆:
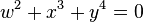
• E₇:
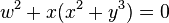
• E₈:

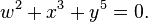
See also

• Brieskorn–Grothendieck resolution

References

• Artin, Michael (1966), "On isolated rational singularities of surfaces", American Journal of Mathematics 88 (1): 129–136, doi:10.2307/2373050, ISSN 0002-9327, JSTOR 2373050, MR 0199191 
• Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius (2004), Compact Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 4, Springer-Verlag, Berlin, ISBN 978-3-540-00832-3, MR 2030225 
• Durfee, Alan H. (1979), "Fifteen characterizations of rational double points and simple critical points", L'Enseignement Mathématique. Revue Internationale. IIe Série 25 (1): 131–163, ISSN 0013-8584, MR 543555 
• du Val, Patrick (1934a), "On isolated singularities of surfaces which do not affect the conditions of adjunction. I", Proceedings of the Cambridge Philosophical Society 30 (4): 453–459, doi:10.1017/S030500410001269X  Zbl entry I
• du Val, Patrick (1934b), "On isolated singularities of surfaces which do not affect the conditions of adjunction. II", Proceedings of the Cambridge Philosophical Society 30 (4): 460–465, doi:10.1017/S0305004100012706  II
• du Val, Patrick (1934c), "On isolated singularities of surfaces which do not affect the conditions of adjunction. III", Proceedings of the Cambridge Philosophical Society 30 (4): 483–491, doi:10.1017/S030500410001272X  III

External links

• Reid, M., The du Val singularities An, Dn, E₆, E₇, E₈ (PDF) 
• Burban, Igor, Du Val Singularities (PDF)