Drinfeld-Sokolov-Wilson equation
The Drinfeld-Sokolov-Wilson equation, or DSW equations, is a system of two coupled nonlinear partial differential equations proposed by Drinfeld, Vladimir Sokolov, and George Wilson[1]:
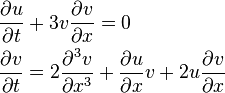
Reference
- ↑ Esmaeil Alibeiki and Ahmad Neyrameh Application of Homotopy Perturbation Method to Nonlinear Drinfeld-Sokolov-Wilson Equation
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759
This article is issued from Wikipedia - version of the Sunday, May 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.