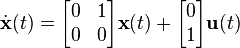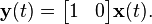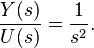Double integrator

In systems and control theory, the double integrator is a canonical example of a second-order control system.^[1] It models the dynamics of a simple mass in one-dimensional space under the effect of a time-varying force input $\textbf{u}$ .

State space representation

The normalized state space model of a double integrator takes the form

\dot{\textbf{x}}(t) = \begin{bmatrix} 0& 1\\ 0& 0\\ \end{bmatrix}\textbf{x}(t) + \begin{bmatrix} 0\\ 1\end{bmatrix}\textbf{u}(t)

\textbf{y}(t) = \begin{bmatrix} 1& 0\end{bmatrix}\textbf{x}(t).

According to this model, the input 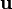$\textbf{u}$ is the second derivative of the output 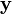$\textbf{y}$ , hence the name double integrator.

Transfer function representation

Taking the Laplace transform of the state space input-output equation, we see that the transfer function of the double integrator is given by

\frac{Y(s)}{U(s)} = \frac{1}{s^2}.

References

↑ Venkatesh G. Rao and Dennis S. Bernstein (2001). "Naive control of the double integrator" (PDF). IEEE Control Systems Magazine. Retrieved 2012-03-04.

This article is issued from Wikipedia - version of the Wednesday, July 02, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.