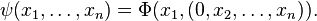Straightening theorem for vector fields

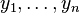In differential calculus, the domain-straightening theorem states that, given a vector field $X$ on a manifold, there exist local coordinates $y_1, \dots, y_n$ such that 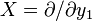$X = \partial / \partial y_1$ in a neighborhood of a point where $X$ is nonzero. The theorem is also known as straightening out of a vector field.

The Frobenius theorem in differential geometry can be considered as a higher-dimensional generalization of this theorem.

Proof

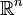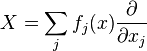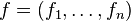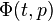It is clear that we only have to find such coordinates at 0 in $\mathbb{R}^n$ . First we write $X = \sum_j f_j(x) {\partial \over \partial x_j}$ where $x$ is some coordinate system at $0$ . Let $f = (f_1, \dots, f_n)$ . By linear change of coordinates, we can assume $f(0) = (1, 0, \dots, 0).$ Let $\Phi(t, p)$ be the solution of the initial value problem 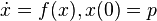$\dot x = f(x), x(0) = p$ and let

\psi(x_1, \dots, x_n) = \Phi(x_1, (0, x_2, \dots, x_n)).

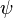$\Phi$ (and thus $\psi$ ) is smooth by smooth dependence on initial conditions in ordinary differential equations. It follows that

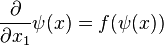{\partial \over \partial x_1} \psi(x) = f(\psi(x))

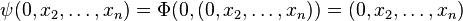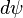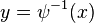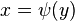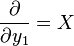and, since $\psi(0, x_2, \dots, x_n) = \Phi(0, (0, x_2, \dots, x_n)) = (0, x_2, \dots, x_n)$ , the differential $d\psi$ is the identity at $0$ . Thus, $y = \psi^{-1}(x)$ is a coordinate system at $0$ . Finally, since $x = \psi(y)$ , we have: ${\partial x_j \over \partial y_1} = f_j(\psi(y)) = f_j(x)$ and so ${\partial \over \partial y_1} = X$ as required.

This article is issued from Wikipedia - version of the Saturday, April 12, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.