Divisibility (ring theory)

In mathematics, the notion of a divisor originally arose within the context of arithmetic of whole numbers. See the article on divisors for this simplest example. With the development of abstract rings, of which the integers are the archetype, the original notion of divisor found a natural extension.

Divisibility is a useful concept for the analysis of the structure of commutative rings because of its relationship with the ideal structure of such rings.

Definition

Let R be a ring,^[1] and let a and b be elements of R. If there exists an element x in R with ax = b, one says that a is a left divisor of b in R and that b is a right multiple of a.^[2] Similarly, if there exists an element y in R with ya = b, one says that a is a right divisor of b and that b is a left multiple of a. One says that a is a two-sided divisor of b if it is both a left divisor and a right divisor of b.

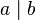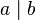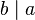When R is commutative, a left divisor, a right divisor and a two-sided divisor coincide, so in this context one says that a is a divisor of b, or that b is a multiple of a, and one writes $a \mid b$ . Elements a and b of an integral domain are associates if both $a \mid b$ and $b \mid a$ . The associate relationship is an equivalence relation on R, and hence divides R into disjoint equivalence classes.

Notes: These definitions make sense in any magma R, but they are used primarily when this magma is the multiplicative monoid of a ring.

Properties

Statements about divisibility in a commutative ring $R$ can be translated into statements about principal ideals. For instance,

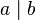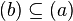One has $a \mid b$ if and only if $(b) \subseteq (a)$ .
Elements a and b are associates if and only if $(a) = (b)$ .
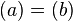An element u is a unit if and only if u is a divisor of every element of R.
An element u is a unit if and only if $(u) = R$ .
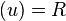If 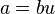$a = b u$ for some unit u, then a and b are associates. If R is an integral domain, then the converse is true.
Let R be an integral domain. If the elements in R are totally ordered by divisibility, then R is called a valuation ring.

In the above, 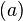$(a)$ denotes the principle ideal of $R$ generated by the element $a$ .

Zero as a divisor, and zero divisors

Some authors require a to be nonzero in the definition of divisor, but this causes some of the properties above to fail.
If one interprets the definition of divisor literally, every a is a divisor of 0, since one can take x = 0. Because of this, it is traditional to abuse terminology by making an exception for zero divisors: one calls an element a in a commutative ring a zero divisor if there exists a nonzero x such that ax = 0.^[3]

Notes

↑ In this article, rings are assumed to have a 1.
↑ Bourbaki, p. 97
↑ Bourbaki, p. 98

References

Bourbaki, N. (1989) [1970], Algebra I, Chapters 1–3, Springer-Verlag, ISBN 9783540642435

This article incorporates material from the Citizendium article "Divisibility (ring theory)", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.

This article is issued from Wikipedia - version of the Thursday, January 29, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.