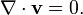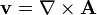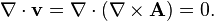Solenoidal vector field
In vector calculus a solenoidal vector field (also known as an incompressible vector field or a divergence free vector field ) is a vector field v with divergence zero at all points in the field:
Properties
The fundamental theorem of vector calculus states that any vector field can be expressed as the sum of an irrotational and a solenoidal field. The condition of zero divergence is satisfied whenever a vector field v has only a vector potential component, because the definition of the vector potential A as:
automatically results in the identity (as can be shown, for example, using Cartesian coordinates):
The converse also holds: for any solenoidal v there exists a vector potential A such that 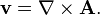 (Strictly speaking, this holds only subject to certain technical conditions on v, see Helmholtz decomposition.)
(Strictly speaking, this holds only subject to certain technical conditions on v, see Helmholtz decomposition.)
The divergence theorem gives the equivalent integral definition of a solenoidal field; namely that for any closed surface, the net total flux through the surface must be zero:
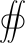
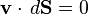 ,
,
where 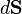 is the outward normal to each surface element.
is the outward normal to each surface element.
Etymology
Solenoidal has its origin in the Greek word for solenoid, which is σωληνοειδές (sōlēnoeidēs) meaning pipe-shaped, from σωλην (sōlēn) or pipe. In the present context of solenoidal it means constrained as if in a pipe, so with a fixed volume.
Examples
- the magnetic field B is solenoidal (see Maxwell's equations);
- the velocity field of an incompressible fluid flow is solenoidal;
- the vorticity field is solenoidal
- the electric field E in neutral regions (
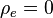 );
); - the current density J where the charge density is unvarying,
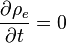 .
.
See also
References
- Aris, Rutherford (1989), Vectors, tensors, and the basic equations of fluid mechanics, Dover, ISBN 0-486-66110-5