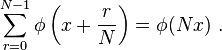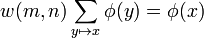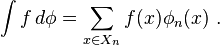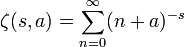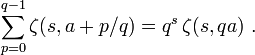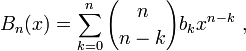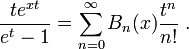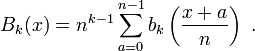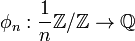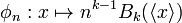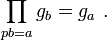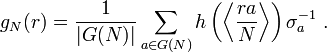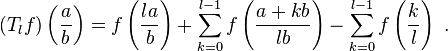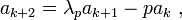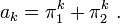Distribution (number theory)

In algebra and number theory, a distribution is a function on a system of finite sets into an abelian group which is analogous to an integral: it is thus the algebraic analogue of a distribution in the sense of generalised function.

The original examples of distributions occur, unnamed, as functions φ on Q/Z satisfying[1]

\sum_{r=0}^{N-1} \phi\left(x + \frac r N\right) = \phi(Nx) \ .

We shall call these ordinary distributions.[2] They also occur in p-adic integration theory in Iwasawa theory.[3]

Let ... → Xn+1 → Xn → ... be a projective system of finite sets with surjections, indexed by the natural numbers, and let X be their projective limit. We give each Xn the discrete topology, so that X is compact. Let φ = (φn) be a family of functions on Xn taking values in an abelian group V and compatible with the projective system:

w(m,n) \sum_{y \mapsto x} \phi(y) = \phi(x)

for some weight function w. The family φ is then a distribution on the projective system X.

A function f on X is "locally constant", or a "step function" if it factors through some Xn. We can define an integral of a step function against φ as

\int f \, d\phi = \sum_{x \in X_n} f(x) \phi_n(x) \ .

The definition extends to more general projective systems, such as those indexed by the positive integers ordered by divisibility. As an important special case consider the projective system Z/n‌Z indexed by positive integers ordered by divisibility. We identify this with the system (1/n)Z/Z with limit Q/Z.

For x in R we let ⟨x⟩ denote the fractional part of x normalised to 0 ≤ ⟨x⟩ < 1, and let {x} denote the fractional part normalised to 0 < {x} ≤ 1.

Examples

Hurwitz zeta function

The multiplication theorem for the Hurwitz zeta function

\zeta(s,a) = \sum_{n=0}^\infty (n+a)^{-s}

gives a distribution relation

\sum_{p=0}^{q-1}\zeta(s,a+p/q)=q^s\,\zeta(s,qa) \ .

Hence for given s, the map 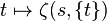t \mapsto \zeta(s,\{t\}) is a distribution on Q/Z.

Bernoulli distribution

Recall that the Bernoulli polynomials Bn are defined by

B_n(x) = \sum_{k=0}^n {n \choose n-k} b_k x^{n-k} \ ,

for n ≥ 0, where bk are the Bernoulli numbers, with generating function

\frac{t e^{xt}}{e^t-1}= \sum_{n=0}^\infty B_n(x) \frac{t^n}{n!} \ .

They satisfy the distribution relation

B_k(x) = n^{k-1} \sum_{a=0}^{n-1} b_k\left({\frac{x+a}{n}}\right)\ .

Thus the map

\phi_n : \frac{1}{n}\mathbb{Z}/\mathbb{Z} \rightarrow \mathbb{Q}

defined by

\phi_n : x \mapsto n^{k-1} B_k(\langle x \rangle)

is a distribution.[4]

Cyclotomic units

The cyclotomic units satisfy distribution relations. Let a be an element of Q/Z prime to p and let ga denote exp(2πia)−1. Then for a≠ 0 we have[5]

\prod_{p b=a} g_b = g_a \ .

Universal distribution

We consider the distributions on Z with values in some abelian group V and seek the "universal" or most general distribution possible.

Stickelberger distributions

Let h be an ordinary distribution on Q/Z taking values in a field F. Let G(N) denote the multiplicative group of Z/N‌Z, and for any function f on G(N) we extend f to a function on Z/N‌Z by taking f to be zero off G(N). Define an element of the group algebra F[G(N)] by

g_N(r) = \frac{1}{|G(N)|} \sum_{a \in G(N)} h\left({\left\langle{\frac{ra}{N}}\right\rangle}\right) \sigma_a^{-1} \ .

The group algebras form a projective system with limit X. Then the functions gN form a distribution on Q/Z with values in X, the Stickelberger distribution associated with h.

p-adic measures

Consider the special case when the value group V of a distribution φ on X takes values in a local field K, finite over Qp, or more generally, in a finite-dimensional p-adic Banach space W over K, with valuation |·|. We call φ a measure if |φ| is bounded on compact open subsets of X.[6] Let D be the ring of integers of K and L a lattice in W, that is, a free D-submodule of W with K⊗L = W. Up to scaling a measure may be taken to have values in L.

Hecke operators and measures

Let D be a fixed integer prime to p and consider ZD, the limit of the system Z/pnD. Consider any eigenfunction of the Hecke operator Tp with eigenvalue λp prime to p. We describe a procedure for deriving a measure of ZD.

Fix an integer N prime to p and to D. Let F be the D-module of all functions on rational numbers with denominator coprime to N. For any prime l not dividing N we define the Hecke operator Tl by

(T_l f)\left(\frac a b\right) = f\left(\frac{la}{b}\right) + \sum_{k=0}^{l-1} f\left({\frac{a+kb}{lb}}\right) - \sum_{k=0}^{l-1} f\left(\frac k l \right) \ .

Let f be an eigenfunction for Tp with eigenvalue λp in D. The quadratic equation X2 − λpX + p = 0 has roots π1, π2 with π1 a unit and π2 divisible by p. Define a sequence a0 = 2, a1 = π1+π2 = λp and

a_{k+2} = \lambda_p a_{k+1} - p a_k \ ,

so that

a_k = \pi_1^k + \pi_2^k \ .

References

  1. ↑ Kubert & Lang (1981) p.1
  2. ↑ Lang (1990) p.53
  3. ↑ Mazur & Swinnerton-Dyer (1972) p. 36
  4. ↑ Lang (1990) p.36
  5. ↑ Lang (1990) p.157
  6. ↑ Mazur & Swinnerton-Dyer (1974) p.37
This article is issued from Wikipedia - version of the Wednesday, February 11, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.