Distribution (differential geometry)
In differential geometry, a discipline within mathematics, a distribution is a subset of the tangent bundle of a manifold satisfying certain properties. Distributions are used to build up notions of integrability, and specifically of a foliation of a manifold.
Even though they share the same name, distributions we discuss in this article have nothing to do with distributions in the sense of analysis.
Definition
Let 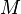 be a
be a  manifold of dimension
manifold of dimension  , and let
, and let 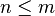 . Suppose that for each
. Suppose that for each  , we assign an
, we assign an  -dimensional subspace
-dimensional subspace 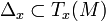 of the tangent space in such a way that for a neighbourhood
of the tangent space in such a way that for a neighbourhood 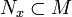 of
of  there exist
there exist  linearly independent smooth vector fields
linearly independent smooth vector fields 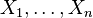 such that for any point
such that for any point 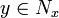 ,
, 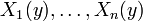 span
span 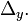 We let
We let 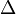 refer to the collection of all the
refer to the collection of all the 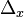 for all
for all  and we then call
and we then call 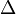 a distribution of dimension
a distribution of dimension  on
on 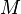 , or sometimes a
, or sometimes a 
 -plane distribution on
-plane distribution on 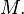 The set of smooth vector fields
The set of smooth vector fields 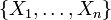 is called a local basis of
is called a local basis of 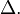
Involutive distributions
We say that a distribution 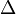 on
on 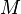 is involutive if for every point
is involutive if for every point  there exists a local basis
there exists a local basis 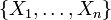 of the distribution in a neighbourhood of
of the distribution in a neighbourhood of  such that for all
such that for all  ,
, ![[X_i,X_j]](../I/m/29a7f7012441cef7ecffb4e7fd6b0d57.png) (the Lie bracket of two vector fields) is in the span of
(the Lie bracket of two vector fields) is in the span of 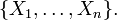 That is, if
That is, if ![[X_i,X_j]](../I/m/29a7f7012441cef7ecffb4e7fd6b0d57.png) is a linear combination of
is a linear combination of 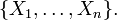 Normally this is written as
Normally this is written as ![[ \Delta , \Delta ] \subset \Delta.](../I/m/55c76e19ccd9c2f814b5fc73397aefb3.png)
Involutive distributions are the tangent spaces to foliations. Involutive distributions are important in that they satisfy the conditions of the Frobenius theorem, and thus lead to integrable systems.
A related idea occurs in Hamiltonian mechanics: two functions f and g on a symplectic manifold are said to be in mutual involution if their Poisson bracket vanishes.
Generalized distributions
A generalized distribution, or Stefan-Sussmann distribution, is similar to a distribution, but the subspaces 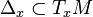 are not required to all be of the same dimension. The definition requires that the
are not required to all be of the same dimension. The definition requires that the 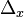 are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of
are determined locally by a set of vector fields, but these will no longer be linearly independent everywhere. It is not hard to see that the dimension of 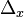 is lower semicontinuous, so that at special points the dimension is lower than at nearby points.
is lower semicontinuous, so that at special points the dimension is lower than at nearby points.
One class of examples is furnished by a non-free action of a Lie group on a manifold, the vector fields in question being the infinitesimal generators of the group action (a free action gives rise to a genuine distribution). Another arises in dynamical systems, where the set of vector fields in the definition is the set of vector fields that commute with a given one. There are also examples and applications in Control theory, where the generalized distribution represents infinitesimal constraints of the system.
References
- William M. Boothby. Section IV. 8. Frobenius's Theorem in An Introduction to Differentiable Manifolds and Riemannian Geometry, Academic Press, San Diego, California, 2003.
- P. Stefan, Accessible sets, orbits and foliations with singularities. Proc. London Math. Soc. 29 (1974), 699-713.
- H.J. Sussmann, Orbits of families of vector fields and integrability of distributions. Trans. Amer. Math. Soc. 180 (1973), 171-188.
External links
- Hazewinkel, Michiel, ed. (2001), "Involutive distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
This article incorporates material from Distribution on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.