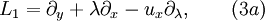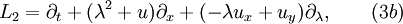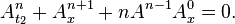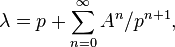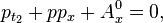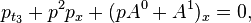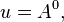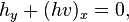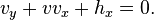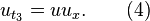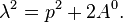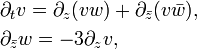Dispersionless equation
Dispersionless (or quasi-classical) limits of integrable partial differential equations (PDE) arise in various problems of mathematics and physics and have been intensively studied in recent literature (see, f.i., [1]-[5]). They typically arise when considering slowly modulated long waves of an integrable dispersive PDE system.
Examples
Dispersionless KP equation
The dispersionless Kadomtsev–Petviashvili equation (dKPE) has the form
It arises from the commutation
of the following pair of 1-parameter families of vector fields
where  is a spectral parameter. The dKPE is the
is a spectral parameter. The dKPE is the  -dispersionless limit of the celebrated Kadomtsev–Petviashvili equation, arising when considering long waves of that system.
-dispersionless limit of the celebrated Kadomtsev–Petviashvili equation, arising when considering long waves of that system.
The Benney Moment Equations
The dispersionless KP system is closely related to the Benney moment hierarchy, each of which is a dispersionless integrable system:
These arise as the consistency condition between
and the simplest two evolutions in the hierarchy are:
The dKP is recovered on setting
and eliminating the other moments, as well as identifying 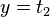 and
and 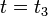 .
.
If one sets 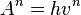 , so that the countably many moments
, so that the countably many moments 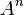 are expressed in terms of just two functions, the classical shallow water equations result:
are expressed in terms of just two functions, the classical shallow water equations result:
These may also be derived from considering slowly modulated wave train solutions of the nonlinear Schrodinger equation. Such 'reductions', expressing the moments in terms of finitely many dependent variables, are described by the Gibbons-Tsarev equation.
Dispersionless Korteweg–de Vries equation
The dispersionless Korteweg–de Vries equation (dKdVE) reads as
It is the dispersionless or quasiclassical limit of the Korteweg–de Vries equation.
It is satisfied by  -independent solutions of the dKP system.
It is also obtainable from the
-independent solutions of the dKP system.
It is also obtainable from the 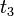 -flow of the Benney hierarchy on setting
-flow of the Benney hierarchy on setting
Dispersionless Novikov–Veselov equation
The dispersionless Novikov-Veselov equation is most commonly written as the following equation for a real-valued function 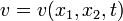 :
:
where the following standard notation of complex analysis is used: 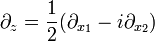 ,
, 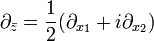 . The function
. The function  here is an auxiliary function, defined uniquely from
here is an auxiliary function, defined uniquely from 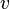 up to a holomorphic summand.
up to a holomorphic summand.
See also
- Integrable systems
- Nonlinear Schrödinger equation
- Nonlinear systems
- Davey–Stewartson equation
- Dispersive partial differential equation
- Kadomtsev–Petviashvili equation
- Korteweg–de Vries equation
References
- Kodama Y., Gibbons J. "Integrability of the dispersionless KP hierarchy", Nonlinear World 1, (1990).
- Zakharov V.E. "Dispersionless limit of integrable systems in 2+1 dimensions", Singular Limits of Dispersive Waves, NATO ASI series, Volume 320, 165-174, (1994).
- Takasaki K., Takebe T. Rev. Math. Phys., 7, 743 (1995)
- Konopelchenko B.G. "Quasiclassical generalized Weierstrass representation and dispersionless DS equation", ArXiv: 0709.4148
- Konopelchenko B.G., Moro A. "Integrable Equations in Nonlinear Geometrical Optics", Studies in Applied Mathematics, 113(4), pp. 325–352 (2004)
- Dunajski M. "Interpolating integrable system". ArXiv: 0804.1234
External links
- Ishimori_system at the dispersive equations wiki
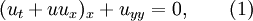
![[L_1, L_2]=0.\qquad (2)](../I/m/eb224c1a56323d7aad32ace8a810a889.png)