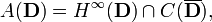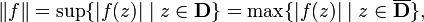Disk algebra

For other uses, see Disc (disambiguation).

In functional and complex analysis, the disk algebra A(D) (also spelled disc algebra) is the set of holomorphic functions

f : D → C,

where D is the open unit disk in the complex plane C, f extends to a continuous function on the closure of D. That is,

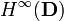A(\mathbf{D}) = H^\infty(\mathbf{D})\cap C(\overline{\mathbf{D}}),

where $H^\infty(\mathbf{D})$ denotes the Banach space of bounded analytic functions on the unit disc D (i.e. a Hardy space). When endowed with the pointwise addition, (f+g)(z)=f(z)+g(z), and pointwise multiplication,

(fg)(z)=f(z)g(z),

this set becomes an algebra over C, since if ƒ and g belong to the disk algebra then so do ƒ + g and ƒg.

Given the uniform norm,

\|f\| = \sup\{|f(z)|\mid z\in \mathbf{D}\}=\max\{ |f(z)|\mid z\in \overline{\mathbf{D}}\},

by construction it becomes a uniform algebra and a commutative Banach algebra.

By construction the disc algebra is a closed subalgebra of the Hardy space H^∞. In contrast to the stronger requirement that a continuous extension to the circle exists, it is a lemma of Fatou that a general element of H^∞ can be radially extended to the circle almost everywhere.

This article is issued from Wikipedia - version of the Saturday, October 04, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.