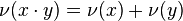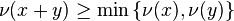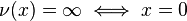Discrete valuation

In mathematics, a discrete valuation is an integer valuation on a field K, that is a function

\nu:K\to\mathbb Z\cup\{\infty\}

satisfying the conditions

\nu(x\cdot y)=\nu(x)+\nu(y)

\nu(x+y)\geq\min\big\{\nu(x),\nu(y)\big\}

\nu(x)=\infty\iff x=0

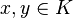for all $x,y\in K$ .

Note that often the trivial valuation which takes on only the values 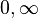$0,\infty$ is explicitly excluded.

A field with a non-trivial discrete valuation is called a discrete valuation field.

Discrete valuation rings and valuations on fields

To every field with discrete valuation 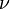$\nu$ we can associate the subring

\mathcal{O}_K := \left\{ x \in K \mid \nu(x) \geq 0 \right\}

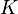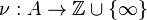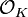of $K$ , which is a discrete valuation ring. Conversely, the valuation $\nu: A \rightarrow \Z\cup\{\infty\}$ on a discrete valuation ring $A$ can be extended in a unique way to a discrete valuation on the quotient field $K=\text{Quot}(A)$ ; the associated discrete valuation ring $\mathcal{O}_K$ is just $A$ .

Examples

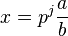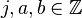For a fixed prime $p$ and for any element $x \in \mathbb{Q}$ different from zero write $x = p^j\frac{a}{b}$ with $j, a,b \in \Z$ such that $p$ does not divide $a,b$ , then $\nu(x) = j$ is a discrete valuation on $\Q$ , called the p-adic valuation.

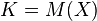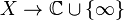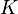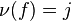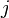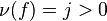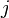Given a Riemann surface $X$ , we can consider the field $K=M(X)$ of meromorphic functions $X\to\C\cup\{\infin\}$ . For a fixed point $p\in X$ , we define a discrete valuation on $K$ as follows: $\nu(f)=j$ if and only if $j$ is the largest integer such that the function $f(z)/(z-p)^j$ can be extended to a holomorphic function at $p$ . This means: if $\nu(f)=j>0$ then $f$ has a root of order $j$ at the point $p$ ; if $\nu(f)=j<0$ then $f$ has a pole of order $-j$ at $p$ . In a similar manner, one also defines a discrete valuation on the function field of an algebraic curve for every regular point $p$ on the curve.

More examples can be found in the article on discrete valuation rings.

References

Fesenko, Ivan B.; Vostokov, Sergei V. (2002), Local fields and their extensions, Translations of Mathematical Monographs 121 (Second ed.), Providence, RI: American Mathematical Society, ISBN 978-0-8218-3259-2, MR 1915966

This article is issued from Wikipedia - version of the Thursday, November 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.