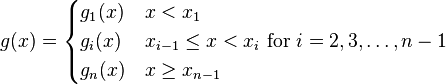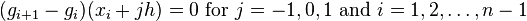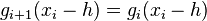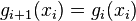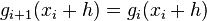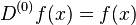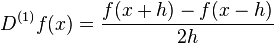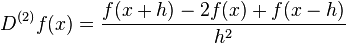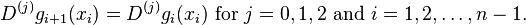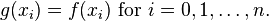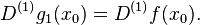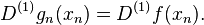Discrete spline interpolation

In the mathematical field of numerical analysis, discrete spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a discrete spline. A discrete spline is a piecewise polynomial such that its central differences are continuous at the knots whereas a spline is a piecewise polynomial such that its derivatives are continuous at the knots. Discrete cubic splines are discrete splines where the central differences of orders 0, 1, and 2 are required to be continuous.^[1]

Discrete splines were introduced by Mangasarin and Schumaker in 1971 as solutions of certain minimization problems involving differences.^[2]

Discrete cubic splines

Let x₁, x₂, . . ., x_n-1 be an increasing set of real numbers. Let g(x) be a piecewise polynomial defined by

g(x)= \begin{cases} g_1(x) & x<x_1 \\ g_i(x) & x_{i-1}\le x < x_i \text{ for } i = 2,3, \ldots, n-1\\ g_n(x) & x\ge x_{n-1} \end{cases}

where g₁(x), . . ., g_n(x) are polynomials of degree 3. Let h > 0. If

(g_{i+1}-g_i)(x_i +jh)=0 \text{ for } j=-1,0,1 \text{ and } i=1,2,\ldots, n-1

then g(x) is called a discrete cubic spline.^[1]

Alternative formulation 1

The conditions defining a discrete cubic spline are equivalent to the following:

g_{i+1}(x_i-h) = g_i(x_i-h)

g_{i+1}(x_i) = g_i(x_i)

g_{i+1}(x_i+h) = g_i(x_i+h)

Alternative formulation 2

The central differences of orders 0, 1, and 2 of a function f(x) are defined as follows:

D^{(0)}f(x) = f(x)

D^{(1)}f(x)=\frac{f(x+h)-f(x-h)}{2h}

D^{(2)}f(x)=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}

The conditions defining a discrete cubic spline are also equivalent to^[1]

D^{(j)}g_{i+1}(x_i)=D^{(j)}g_i(x_i) \text{ for } j=0,1,2 \text{ and } i=1,2, \ldots, n-1.

This states that the central differences 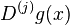$D^{(j)}g(x)$ are continuous at x_i.

Example

Let x₁ = 1 and x₂ = 2 so that n = 3. The following function defines a discrete cubic spline:^[1]

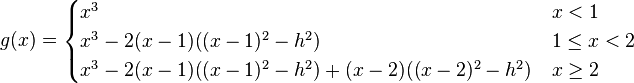
$g(x) = \begin{cases} x^3 & x<1 \\ x^3 - 2(x-1)((x-1)^2-h^2) & 1\le x < 2\\ x^3 - 2(x-1)((x-1)^2-h^2)+(x-2)((x-2)^2-h^2) & x \ge 2 \end{cases}$

Discrete cubic spline interpolant

Let x₀ < x₁ and x_n > x_n-1 and f(x) be a function defined in the closed interval [x₀ - h, x_n + h]. Then there is a unique cubic discrete spline g(x) satisfying the following conditions:

g(x_i) = f(x_i) \text{ for } i=0,1,\ldots, n.

D^{(1)}g_1(x_0) = D^{(1)}f(x_0).

D^{(1)}g_n(x_n) = D^{(1)}f(x_n).

This unique discrete cubic spline is the discrete spline interpolant to f(x) in the interval [x₀ - h, x_n + h]. This interpolant agrees with the values of f(x) at x₀, x₁, . . ., x_n.

Applications

Discrete cubic splines were originally introduced as solutions of certain minimization problems.^[1]^[2]
They have applications in computing nonlinear splines.^[1]^[3]
They are used to obtain approximate solution of a second order boundary value problem.^[4]
Discrete interpolatory splines have been used to construct biorthogonal wavelets.^[5]

References

1 2 3 4 5 6 Tom Lyche (1979). "Discrete Cubic Spline Interpolation". BIT 16: 281–290. doi:10.1007/bf01932270.
1 2 Mangasarian, O. L. and Schumaker, L. L. (1971). "Discrete splines via mathematical programming". SIAM J. Control. 9: 174–183. doi:10.1137/0309015.
↑ Michael A Malcolm (April 1977). "Onion of nolinear spline functionsat the comput". SIAM Journal of Numerical Analysis 14 (2).
↑ Fengmin Chen, Wong, P.J.Y. (Dec 2012). "Solving second order boundary value problems by discrete cubic splines". Control Automation Robotics & Vision (ICARCV), 2012 12th International Conference: 1800–1805.
↑ Averbuch, A.Z., Pevnyi, A.B., Zheludev, V.A. (Nov 2001). "Biorthogonal Butterworth wavelets derived from discrete interpolatory splines". Signal Processing, IEEE Transactions 49 (11): 2682–2692. doi:10.1109/78.960415.

This article is issued from Wikipedia - version of the Tuesday, January 19, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.