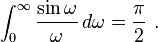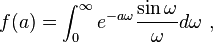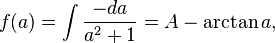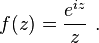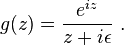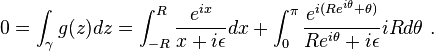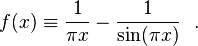Dirichlet integral

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.

One of those is the definite integral of the Sinc function,

\int_0^\infty \frac{\sin \omega}{\omega}\,d\omega = \frac{\pi}{2} ~.

This integral is not absolutely convergent, and so the integral is not even defined in the sense of Lebesgue integration, but it is defined in the sense of the improper Riemann integral or the Henstock–Kurzweil integral.^[1] The value of the integral (in the Riemann or Henstock sense) can be derived in various ways. For example, the value can be determined from attempts to evaluate a double improper integral, or by using differentiation under the integral sign.

Evaluation

Double improper integral method

Pre-knowledge of properties of Laplace transforms allows us to evaluate this Dirichlet integral succinctly in the following manner:

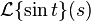\int_0^\infty\frac{\sin t}{t}\, dt=\int_{0}^{\infty}\mathcal{L}\{\sin t\}(s)\; ds=\int_{0}^{\infty}\frac{1}{s^{2}+1}\, ds=\arctan s\bigg|_{0}^{\infty}=\frac{\pi}{2},

where $\mathcal{L}\{\sin t\}(s)$ is the Laplace transform of the function, sin $t$ . Applying Euler's formula, then integrating, making the denominator real, and taking the imaginary part, we see the Laplace transform is the function 1/( $s$ ²+1), a function of the Laplace transform variable, $s$ .

This is equivalent to attempting to evaluate the same double definite integral in two different ways, by reversal of the order of integration, viz.,

\left ( I_1=\int_0^\infty {\int _0^\infty e^{-st} \sin t\, dt}\, ds\right ) = \left ( I_2=\int_0^\infty {\int _0^\infty e^{-st} \sin t\, ds} \, dt \right ),

\left ( I_1=\int_0^\infty {\frac{1}{s^2+1}}\, ds = \frac{\pi}{2}\right ) = \left ( I_2=\int_0^\infty \sin t\, \frac{1}{t} \, dt\right ) \text{, provided } s>0.

Differentiation under the integral sign

First rewrite the integral as a function of the additional variable $a$ . Let

f(a)=\int_0^\infty e^{-a\omega} \frac{\sin \omega}{\omega} d\omega ~,

so that we need evaluate $f$ (0).

Differentiate with respect to $a$ and apply the Leibniz integral rule to obtain

\frac{df}{da}=\frac{d}{da}\int_0^\infty e^{-a\omega} \frac{\sin \omega}{\omega} d\omega = \int_0^\infty \frac{\partial}{\partial a}e^{-a\omega}\frac{\sin \omega}{\omega} d\omega = -\int_0^\infty e^{-a\omega} \sin \omega \,d\omega = -\mathcal{L}\{\sin \omega\}(a).

This integral was evaluated without proof, above, based on Laplace transform tables; we derive it this time. It is made much simpler by recalling Euler's formula,

\! e^{i\omega}=\cos \omega + i\sin \omega ,

so then

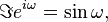\Im e^{i\omega}=\sin \omega,

where

\Im

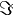represents the imaginary part.

\therefore \qquad \frac{df}{da}=-\Im\int_0^\infty e^{-a\omega}e^{i\omega}d\omega=\Im\frac{1}{-a+i}=\Im\frac{-a-i}{a^2+1}=\frac{-1}{a^2+1} \qquad \text{, given that } a > 0 .

Integrating with respect to $a$ ,

f(a) = \int \frac{-da}{a^2+1} = A - \arctan a,

where $A$ is a constant to be determined. As $f$ (+∞)=0,

\therefore \qquad A = \arctan (+\infty) = \frac{\pi}{2} + m\pi,

\therefore \qquad f(0)=\lim _{a \to 0^+} f(a) = \frac{\pi}{2} + m\pi - \arctan 0 = \frac{\pi}{2} + n\pi,

for integers $m$ and $n$ .

It is easy to see that $n$ has to be zero, by analyzing easily observed bounds for this integral,

0<\int _0^\infty \frac {\sin x}{x}dx < \int _0^\pi \frac {\sin x}{x}dx < \pi ~.

The left and right bounds can be derived by dividing the integrated region [0, ∞] into periodic intervals, over which the integrals have zero value:

Left bound: $\int_0^{\infty} \frac{\sin x}{x}dx = \sum_{n=0}^{n = \infty} \int_{2\pi n}^{2\pi (n+1)} \frac{\sin x}{x}dx = \sum_{n=0}^{n = \infty} \int_{0}^{2\pi} \frac{\sin x}{2\pi n + x}dx > \sum_{n=0}^{n = \infty} \int_{0}^{2\pi} \frac{\sin x}{2\pi (n+1)}dx = 0$

Right bound: $\int_0^{\infty} \frac{\sin x}{x}dx = \int_0^{\pi} \frac{\sin x}{x}dx + \int_{\pi}^{\infty} \frac{\sin x}{x}dx$

The second term can be written as

\sum_{n=1}^{\infty}\int_{\pi(2n-1)}^{\pi(2n+1)}\frac{\sin x}{x} \ dx < \sum_{n=1}^{\infty} \frac{1}{2\pi n} (\int_{\pi(2n-1)}^{2n\pi} \sin x \ dx + \int_{2n\pi}^{\pi(2n+1)}\sin x \ dx) = \sum_{n=1}^{\infty} \frac{1}{2\pi n} \int_{\pi(2n-1)}^{\pi(2n+1)} \sin x \ dx ~.

Clearly,

\int_{\pi(2n-1)}^{\pi(2n+1)} \sin x \ dx=0 ~.

Thus

\int _\pi^\infty \frac {\sin x}{x}dx < 0 ~.

This completes the proof.

This result may be further extended with the introduction of another variable, $b$ , first noting that the Sinc function, sin $x / x$ , is an even function, and therefore

\int_0^\infty \frac{\sin x}{x}\,dx = \int_{-\infty}^0 \frac{\sin x}{x}\,dx = -\int_0^{-\infty} \frac{\sin x}{x}\,dx~,

so then

g(b)\equiv \int_0^\infty \frac{\sin b\,\omega}{\omega}\,d\omega = \int_0^{b\,\infty} \frac{\sin b\,\omega}{b\,\omega}\,d(b\,\omega) = \int_0^{\sgn \! b\cdot\infty} \frac{\sin x}{x}\,dx = \sgn b \int_0^\infty \frac{\sin x}{x}\,dx = \frac{\pi}{2}\,\sgn b= {\pi b \over 2 |b|} ~.

Complex integration

The same result can be obtained via complex integration. Consider

f(z)=\frac{e^{iz}}{z} ~.

As a function of the complex variable $z$ , it has a simple pole at the origin, which prevents the application of Jordan's lemma, whose other hypotheses are satisfied.

Define then a new function^[2] $g (z)$ as follows,

g(z)=\frac{e^{iz}}{z +i\epsilon} ~.

The pole has been moved away from the real axis, so $g (z)$ can be integrated along the semicircle of radius $R$ centered at $z$ =0 and closed on the real axis; then the limit ε→0 should be taken.

The complex integral is zero by the residue theorem, as there are no poles inside the integration path

0 = \int_\gamma g(z) dz = \int_{-R}^R \frac{e^{ix}}{x +i\epsilon} dx + \int_{0}^{\pi} \frac{e^{i(Re^{i\theta} + \theta)}}{Re^{i\theta} +i\epsilon} iR d\theta ~.

The second term vanishes as $R$ goes to infinity; for arbitrarily small ε, the Sokhotski–Plemelj theorem applied to the first one yields

0= \mathrm{P.V.} \int \frac{e^{ix}}{x} dx - \pi i \int_{-\infty}^{\infty}\delta(x) e^{ix} dx

where P.V. indicates the Cauchy principal value.

By taking the imaginary part on both sides and noting that the Sinc function sinc(x) is even and by definition sinc(0)=1, we get the desired result

\lim_{\epsilon\rightarrow 0}\int_\epsilon^{\infty} \frac{\sin(x)}{x} dx = \int_0^{\infty} \frac{\sin(x)}{x} dx = \frac{\pi}{2} ~.

Via the Dirichlet kernel

Let

D_n(x)=\sum_{k=-n}^n e^{2 \pi ikx}=\frac{\sin\left(\left(2n +1\right)\pi x \right)}{\sin(\pi x)}

be the Dirichlet kernel.

This is clearly symmetric around zero, that is,

D_n(-x) = D_n(x)

for all $x$ , and

\int_{-1/2}^{1/2}D_n(x)dx = \sum_{|k|<n}\int_{-1/2}^{1/2}e^{2 \pi ikx}dx = 1 + \sum_{0<|k|<n}\frac{1}{2 \pi ik} \left( e^{\pi i k} - e^{- \pi i k}\right) = 1 + \sum_{0<|k|<n}\frac{\sin(\pi k)}{\pi k} = 1

since sin( $πk$ ) = 0 ∀ $k$ ∈ ℤ. Define

f(x) \equiv \frac{1}{\pi x} - \frac{1}{\sin(\pi x)} ~~.

This is continuous on the interval [0, 1/2], so it is bounded by | $f (x)$ | ≤ $A$ , ∀ $x$ , for some constant $A$ ∈ ℝ_≥0, and hence by the Riemann-Lebesgue Lemma,

\int_0^\frac{1}{2}f(x)\sin((2n+1)\pi x)dx \rightarrow 0

as $n$ →∞. Therefore

\begin{align}\int_0^\infty \frac{\sin(x)}{x} dx & = \lim_{n\rightarrow \infty} \int_0^{(2n+1)\frac{\pi}{2}}\frac{\sin(x)}{x}dx \\ & = \lim_{n\rightarrow\infty}\int_0^\frac{1}{2} \frac{\sin((2n+1)\pi x)}{x} dx \qquad \text{ by substituting }x\mapsto (2n+1)\pi x.\\ & = \pi\lim_{n\rightarrow\infty}\int_0^\frac{1}{2}\sin((2n+1)\pi x)\left(f(x)+\frac{1}{\sin(\pi x)}\right)dx \\ & = \pi\lim_{n\rightarrow\infty}\left(\int_0^\frac{1}{2}f(x)\sin(2n+1)\pi x)dx + \frac{1}{2}\int_{-\frac{1}{2}}^\frac{1}{2} D_n(x) dx\right) \\ & = \frac{\pi}{2}\end{align}

by the above.

Notes

↑ Robert G. Bartle, Return to the Riemann Integral, The American Mathematical Monthly, vol. 103, 1996, pp. 625-632.
↑ Appel, Walter. Mathematics for Physics and Physicists. Princeton University Press, 2007, p. 226.

External links

Weisstein, Eric W., "Dirichlet Integrals", MathWorld.

This article is issued from Wikipedia - version of the Saturday, February 13, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.