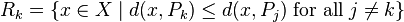Voronoi diagram

20 points and their Voronoi cells (larger version below).

In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane. That set of points (called seeds, sites, or generators) is specified beforehand, and for each seed there is a corresponding region consisting of all points closer to that seed than to any other. These regions are called Voronoi cells. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.

It is named after Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi diagrams have practical and theoretical applications to a large number of fields, mainly in science and technology but also including visual art.^[1]^[2]

The simplest case

In the simplest case, shown in the first picture, we are given a finite set of points {p₁, …, p_n} in the Euclidean plane. In this case each site p_k is simply a point, and its corresponding Voronoi cell R_k consists of every point whose distance to p_k is less than or equal to its distance to any other p_k. Each such cell is obtained from the intersection of half-spaces, and hence it is a convex polygon. The line segments of the Voronoi diagram are all the points in the plane that are equidistant to the two nearest sites. The Voronoi vertices (nodes) are the points equidistant to three (or more) sites.

Formal definition

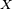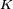Let $\scriptstyle X$ be a metric space with distance function $\scriptstyle d$ . Let $\scriptstyle K$ be a set of indices and let 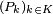$\scriptstyle (P_k)_{k \in K}$ be a tuple (ordered collection) of nonempty subsets (the sites) in the space 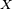$\scriptstyle X$ . The Voronoi cell, or Voronoi region, 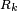$\scriptstyle R_k$ , associated with the site 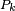$\scriptstyle P_k$ is the set of all points in 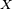$\scriptstyle X$ whose distance to 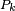$\scriptstyle P_k$ is not greater than their distance to the other sites 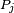$\scriptstyle P_j$ , where 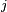$\scriptstyle j$ is any index different from $\scriptstyle k$ . 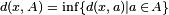In other words, if $\scriptstyle d(x,\, A) \;=\; \inf\{d(x,\, a) \mid a \,\in\, A\}$ denotes the distance between the point $\scriptstyle x$ and the subset $\scriptstyle A$ , then

R_k = \{x \in X \mid d(x, P_k) \leq d(x, P_j)\; \text{for all}\; j \neq k\}

The Voronoi diagram is simply the tuple of cells 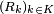$\scriptstyle (R_k)_{k \in K}$ . In principle some of the sites can intersect and even coincide (an application is described below for sites representing shops), but usually they are assumed to be disjoint. In addition, infinitely many sites are allowed in the definition (this setting has applications in geometry of numbers and crystallography), but again, in many cases only finitely many sites are considered.

In the particular case where the space is a finite-dimensional Euclidean space, each site is a point, there are finitely many points and all of them are different, then the Voronoi cells are convex polytopes and they can be represented in a combinatorial way using their vertices, sides, 2-dimensional faces, etc. Sometimes the induced combinatorial structure is referred to as the Voronoi diagram. However, in general the Voronoi cells may not be convex or even connected.

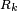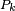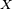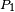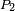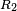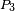In the usual Euclidean space, we can rewrite the formal definition in usual terms. Each Voronoi polygon $\scriptstyle R_k$ is associated with a generator point $\scriptstyle P_k$ . Let $\scriptstyle X$ the set of all points in the Euclidean space. 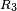Let $\scriptstyle P_1$ be a point that generates its Voronoi region $\scriptstyle R_1$ , $\scriptstyle P_2$ that generates $\scriptstyle R_2$ , and $\scriptstyle P_3$ that generates $\scriptstyle R_3$ , and so on. Then, as expressed by Tran et al^[3] "all locations in the Voronoi polygon are closer to the generator point of that polygon than any other generator point in the Voronoi diagram in Euclidian plane".

Illustration

As a simple illustration, consider a group of shops in a city. Suppose we want to estimate the number of customers of a given shop. With all else being equal (price, products, quality of service, etc.), it is reasonable to assume that customers choose their preferred shop simply by distance considerations: they will go to the shop located nearest to them. In this case the Voronoi cell 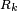$\scriptstyle R_k$ of a given shop 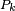$\scriptstyle P_k$ can be used for giving a rough estimate on the number of potential customers going to this shop (which is modeled by a point in our city).

For most cities, the distance between points can be measured using the familiar Euclidean distance: $\ell_2 = d\left[\left(a_1, a_2\right), \left(b_1, b_2\right)\right] = \sqrt{\left(a_1 - b_1\right)^2 + \left(a_2 - b_2\right)^2}$ or the Manhattan distance: $d\left[\left(a_1, a_2\right), \left(b_1, b_2\right)\right] = \left|a_1 - b_1\right| + \left|a_2 - b_2\right|$ . The corresponding Voronoi diagrams look different for different distance metrics.

Voronoi diagrams of 20 points under two different metrics

Euclidean distance

Manhattan distance

Properties

The dual graph for a Voronoi diagram (in the case of a Euclidean space with point sites) corresponds to the Delaunay triangulation for the same set of points.
The closest pair of points corresponds to two adjacent cells in the Voronoi diagram.
Assume the setting is the Euclidean plane and a group of different points are given. Then two points are adjacent on the convex hull if and only if their Voronoi cells share an infinitely long side.
If the space is a normed space and the distance to each site is attained (e.g., when a site is a compact set or a closed ball), then each Voronoi cell can be represented as a union of line segments emanating from the sites.^[4] As shown there, this property does not necessarily hold when the distance is not attained.
Under relatively general conditions (the space is a possibly infinite-dimensional uniformly convex space, there can be infinitely many sites of a general form, etc.) Voronoi cells enjoy a certain stability property: a small change in the shapes of the sites, e.g., a change caused by some translation or distortion, yields a small change in the shape of the Voronoi cells. This is the geometric stability of Voronoi diagrams.^[5] As shown there, this property does not hold in general, even if the space is two-dimensional (but non-uniformly convex, and, in particular, non-Euclidean) and the sites are points.

History and research

Informal use of Voronoi diagrams can be traced back to Descartes in 1644. Peter Gustav Lejeune Dirichlet used 2-dimensional and 3-dimensional Voronoi diagrams in his study of quadratic forms in 1850. British physician John Snow used a Voronoi diagram in 1854 to illustrate how the majority of people who died in the Soho cholera epidemic lived closer to the infected Broad Street pump than to any other water pump.

Voronoi diagrams are named after Russian and Ukrainian mathematician Georgy Fedosievych Voronyi (or Voronoy) who defined and studied the general n-dimensional case in 1908. Voronoi diagrams that are used in geophysics and meteorology to analyse spatially distributed data (such as rainfall measurements) are called Thiessen polygons after American meteorologist Alfred H. Thiessen. In condensed matter physics, such tessellations are also known as Wigner–Seitz unit cells. Voronoi tessellations of the reciprocal lattice of momenta are called Brillouin zones. For general lattices in Lie groups, the cells are simply called fundamental domains. In the case of general metric spaces, the cells are often called metric fundamental polygons. Other equivalent names for this concept (or particular important cases of it): Voronoi polyhedra, Voronoi polygons, domain(s) of influence, Voronoi decomposition, Voronoi tessellation(s), Dirichlet tessellation(s).

Examples

This is a slice of the Voronoi diagram of a random set of points in a 3D box. In general a cross section of a 3D Voronoi tessellation is not a 2D Voronoi tessellation itself. (The cells are all convex polyhedra.)

Voronoi tessellations of regular lattices of points in two or three dimensions give rise to many familiar tessellations.

A 2D lattice gives an irregular honeycomb tessellation, with equal hexagons with point symmetry; in the case of a regular triangular lattice it is regular; in the case of a rectangular lattice the hexagons reduce to rectangles in rows and columns; a square lattice gives the regular tessellation of squares; note that the rectangles and the squares can also be generated by other lattices (for example the lattice defined by the vectors (1,0) and (1/2,1/2) gives squares). See here for a dynamic visual example.
A simple cubic lattice gives the cubic honeycomb.
A hexagonal close-packed lattice gives a tessellation of space with trapezo-rhombic dodecahedra.
A face-centred cubic lattice gives a tessellation of space with rhombic dodecahedra.
A body-centred cubic lattice gives a tessellation of space with truncated octahedra.
Parallel planes with regular triangular lattices aligned with each other's centers give the hexagonal prismatic honeycomb.
Certain body centered tetragonal lattices give a tessellation of space with rhombo-hexagonal dodecahedra.

For the set of points (x, y) with x in a discrete set X and y in a discrete set Y, we get rectangular tiles with the points not necessarily at their centers.

Higher-order Voronoi diagrams

Although a normal Voronoi cell is defined as the set of points closest to a single point in S, an nth-order Voronoi cell is defined as the set of points having a particular set of n points in S as its n nearest neighbors. Higher-order Voronoi diagrams also subdivide space.

Higher-order Voronoi diagrams can be generated recursively. To generate the n^th-order Voronoi diagram from set S, start with the (n − 1)^th-order diagram and replace each cell generated by X = {x₁, x₂, ..., x_n−1} with a Voronoi diagram generated on the set S − X.

Farthest-point Voronoi diagram

For a set of n points the (n − 1)^th-order Voronoi diagram is called a farthest-point Voronoi diagram.

For a given set of points S = {p₁, p₂, ..., p_n} the farthest-point Voronoi diagram divides the plane into cells in which the same point of P is the farthest point. Note that a point of P has a cell in the farthest-point Voronoi diagram if and only if it is a vertex of the convex hull of P. Thus, let H = {h₁, h₂, ..., h_k} be the convex hull of P we define the farthest-point Voronoi diagram as the subdivision of the plane into k cells, one for each point in H, with the property that a point q lies in the cell corresponding to a site h_i if and only if dist(q, h_i) > dist(q, p_j) for each p_j ∈ S with h_i ≠ p_j. Where dist(p, q) is the Euclidean distance between two points p and q.^[6]^[7]

Generalizations and variations

As implied by the definition, Voronoi cells can be defined for metrics other than Euclidean (such as the Mahalanobis or Manhattan) distances. However, in these cases the boundaries of the Voronoi cells may be more complicated than in the Euclidean case, since the equidistant locus for two points may fail to be subspace of codimension 1, even in the 2-dimensional case.

Approximate Voronoi diagram of a set of points. Notice the blended colors in the fuzzy boundary of the Voronoi cells.

A weighted Voronoi diagram is the one in which the function of a pair of points to define a Voronoi cell is a distance function modified by multiplicative or additive weights assigned to generator points. In contrast to the case of Voronoi cells defined using a distance which is a metric, in this case some of the Voronoi cells may be empty. A power diagram is a type of Voronoi diagram defined from a set of circles using the power distance; it can also be thought of as a weighted Voronoi diagram in which a weight defined from the radius of each circle is added to the squared distance from the circle's center.^[8]

The Voronoi diagram of n points in d-dimensional space requires 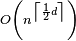$\scriptstyle O\left(n^{\left\lceil \frac{1}{2}d \right\rceil}\right)$ storage space. Therefore, Voronoi diagrams are often not feasible for d > 2. An alternative is to use approximate Voronoi diagrams, where the Voronoi cells have a fuzzy boundary, which can be approximated.^[9] Another alternative is when any site is a fuzzy circle and as a result the cells become fuzzy too.^[10]

Voronoi diagrams are also related to other geometric structures such as the medial axis (which has found applications in image segmentation, optical character recognition, and other computational applications), straight skeleton, and zone diagrams. Besides points, such diagrams use lines and polygons as seeds. By augmenting the diagram with line segments that connect to nearest points on the seeds, a planar subdivision of the environment is obtained.^[11] This structure can be used as a navigation mesh for path-finding through large spaces. The navigation mesh has been generalized to support 3D multi-layered environments, such as an airport or a multi-storey building.^[12]

Applications

In astrophysics, Voronoi diagrams are used to generate adaptative smoothing zones on images, adding signal fluxes on each one. The main objective for these procedures is to maintain a relatively constant signal-to-noise ratio on all the image.

John Snow's original diagram

In epidemiology, Voronoi diagrams can be used to correlate sources of infections in epidemics. One of the early applications of Voronoi diagrams was implemented by John Snow to study the 1854 Broad Street cholera outbreak in Soho, England. He showed the correlation between residential areas on the map of Central London whose residents had been using a specific water pump, and the areas with most deaths due to the outbreak.
A point location data structure can be built on top of the Voronoi diagram in order to answer nearest neighbor queries, where one wants to find the object that is closest to a given query point. Nearest neighbor queries have numerous applications. For example, one might want to find the nearest hospital, or the most similar object in a database. A large application is vector quantization, commonly used in data compression.
In geometry, Voronoi diagrams can be used to find the largest empty circle amid a set of points, and in an enclosing polygon; e.g. to build a new supermarket as far as possible from all the existing ones, lying in a certain city.
Voronoi diagrams together with farthest-point Voronoi diagrams are used for efficient algorithms to compute the roundness of a set of points.^[6]
The Voronoi approach is also put to good use in the evaluation of circularity/roundness while assessing the dataset from a coordinate-measuring machine.
In aviation, Voronoi diagrams are superimposed on oceanic plotting charts to identify the nearest airfield for in-flight diversion, as an aircraft progresses through its flight plan.
In networking, Voronoi diagrams can be used in derivations of the capacity of a wireless network.
In hydrology, Voronoi diagrams are used to calculate the rainfall of an area, based on a series of point measurements. In this usage, they are generally referred to as Thiessen polygons.
In ecology, Voronoi diagrams are used to study the growth patterns of forests and forest canopies, and may also be helpful in developing predictive models for forest fires.
In architecture, Voronoi patterns were the basis for the winning entry for redevelopment of The Arts Centre Gold Coast.^[13]
In computational chemistry, Voronoi cells defined by the positions of the nuclei in a molecule are used to compute atomic charges. This is done using the Voronoi deformation density method.
In polymer physics, Voronoi diagrams can be used to represent free volumes of polymers.
In materials science, polycrystalline microstructures in metallic alloys are commonly represented using Voronoi tessellations. In solid state physics, the Wigner-Seitz cell is the Voronoi tessellation of a solid, and the Brillouin zone is the Voronoi tessellation of reciprocal (wave number) space of crystals which have the symmetry of a space group.
In mining, Voronoi polygons are used to estimate the reserves of valuable materials, minerals, or other resources. Exploratory drillholes are used as the set of points in the Voronoi polygons.
In computer graphics, Voronoi diagrams are used to calculate 3D shattering / fracturing geometry patterns. It is also used to procedurally generate organic or lava-looking textures.
In autonomous robot navigation, Voronoi diagrams are used to find clear routes. If the points are obstacles, then the edges of the graph will be the routes furthest from obstacles (and theoretically any collisions).
In machine learning, Voronoi diagrams are used to do 1-NN classifications.^[14]
In biology, Voronoi diagrams are used to model a number of different biological structures, including cells^[15] and bone microarchitecture.^[16]
In user interface development, Voronoi patterns can be used to compute the best hover state for a given point.^[17]
In computational fluid dynamics, the Voronoi tessellation of a set of points can be used to define the computational domains used in finite volume methods, e.g. as in the moving-mesh cosmology code AREPO.^[18]

Algorithms

Direct algorithms:

Fortune's algorithm, an O(n log(n)) algorithm for generating a Voronoi diagram from a set of points in a plane.
Lloyd's algorithm, aka k-means clustering, produces a Voronoi tessellation in a space of arbitrary dimensions

Starting with a Delaunay triangulation (obtain the dual):

Bowyer–Watson algorithm, an O(n log(n)) to O(n²) algorithm for generating a Delaunay triangulation in any number of dimensions, from which the Voronoi diagram can be obtained.

Notes

↑ Franz Aurenhammer (1991). Voronoi Diagrams – A Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys, 23(3):345–405, 1991
↑ Atsuyuki Okabe, Barry Boots, Kokichi Sugihara & Sung Nok Chiu (2000). Spatial Tessellations – Concepts and Applications of Voronoi Diagrams. 2nd edition. John Wiley, 2000, 671 pages ISBN 0-471-98635-6
↑ Q.T.Tran, D.Tainar and M.Safar (2009) "Transactions on Large-Scale Data- and Knowledge-Centered Systems", pag357. ISBN 9783642037214.
↑ Daniel Reem, An algorithm for computing Voronoi diagrams of general generators in general normed spaces, In Proceedings of the sixth International Symposium on Voronoi Diagrams in science and engineering (ISVD 2009), 2009, pp. 144–152
↑ Daniel Reem, The geometric stability of Voronoi diagrams with respect to small changes of the sites, Full version: arXiv 1103.4125 (2011), Extended abstract in Proceedings of the 27th Annual ACM Symposium on Computational Geometry (SoCG 2011), pp. 254–263
1 2 Mark de Berg; Marc van Kreveld; Mark Overmars; Otfried Schwarzkopf (2008). Computational Geometry (Third ed.). Springer-Verlag. ISBN 978-3-540-77974-2. 7.4 Farthest-Point Voronoi Diagrams. Includes a description of the algorithm.
↑ Skyum, Sven (18 February 1991). "A simple algorithm for computing the smallest enclosing circle". Information Processing Letters 37 (3): 121–125. doi:10.1016/0020-0190(91)90030-L. , contains a simple algorithm to compute the farthest-point Voronoi diagram.
↑ Edelsbrunner, Herbert (1987), "13.6 Power Diagrams", Algorithms in Combinatorial Geometry, EATCS Monographs on Theoretical Computer Science 10, Springer-Verlag, pp. 327–328 .
↑ S. Arya, T. Malamatos, and D. M. Mount, Space-Efficient Approximate Voronoi Diagrams, Proc. 34th ACM Symp. on Theory of Computing (STOC 2002), pp. 721–730.
↑ Jooyandeh, Mohammadreza; Mohades, Ali; Mirzakhah, Maryam (2009). "Uncertain Voronoi Diagram" (PDF). Information Processing Letters (Elsevier) 109 (13): 709–712. doi:10.1016/j.ipl.2009.03.007.
↑ Geraerts, Roland (2010), Planning Short Paths with Clearance using Explicit Corridors (PDF), International Conference on Robotics and Automation, IEEE, pp. 1997–2004 .
↑ van Toll, Wouter G.; Cook IV, Atlas F.; Geraerts, Roland (2011), Navigation Meshes for Realistic Multi-Layered Environments (PDF), International Conference on Intelligent Robots and Systems, IEEE/RSJ, pp. 3526–3532 .
↑ "GOLD COAST CULTURAL PRECINCT". ARM Architecture.
↑ Tom M. Mitchell (1997). Machine Learning (International Edition 1997 ed.). McGraw-Hill. p. 233. ISBN 0-07-042807-7.
↑ Martin Bock (2009). "Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics".
↑ Hui Li (2012). "Spatial Modeling of Bone Microarchitecture".
↑ "User Interface Algorithms".
↑ Springel, Volker (2010). "E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh". MNRAS 401 (2): 791–851. doi:10.1111/j.1365-2966.2009.15715.x.

References

G. Lejeune Dirichlet (1850). "Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen". Journal für die Reine und Angewandte Mathematik 40: 209–227.
Voronoi, Georgy (1908). "Nouvelles applications des paramètres continus à la théorie des formes quadratiques". Journal für die Reine und Angewandte Mathematik 133 (133): 97–178. doi:10.1515/crll.1908.133.97.
Atsuyuki Okabe, Barry Boots, Kokichi Sugihara & Sung Nok Chiu (2000). Spatial Tessellations – Concepts and Applications of Voronoi Diagrams. 2nd edition. John Wiley, 2000, 671 pages, ISBN 0-471-98635-6
Franz Aurenhammer, Rolf Klein & Der-Tsai Lee (2013) "Voronoi Diagrams and Delaunay Triangulations". World Scientific, 2013, 337 pages, ISBN 978-9814447638
Bowyer, Adrian (1981). "Computing Dirichlet tessellations". Comput. J. 24 (2): 162–166. doi:10.1093/comjnl/24.2.162.
Reem, Daniel (2009). "An algorithm for computing Voronoi diagrams of general generators in general normed spaces". Proceedings of the sixth International Symposium on Voronoi Diagrams in science and engineering (ISVD 2009). pp. 144–152. doi:10.1109/ISVD.2009.23.

Daniel Reem (2011). The geometric stability of Voronoi diagrams with respect to small changes of the sites. Full version: arXiv 1103.4125 (2011), Extended abstract: in Proceedings of the 27th Annual ACM Symposium on Computational Geometry (SoCG 2011), pp. 254–263.
Watson, David F. (1981). "Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopes". Comput. J. 24 (2): 167–172. doi:10.1093/comjnl/24.2.167.
Mark de Berg; Marc van Kreveld; Mark Overmars; Otfried Schwarzkopf (2000). Computational Geometry (2nd revised ed.). Springer-Verlag. ISBN 3-540-65620-0. Chapter 7: Voronoi Diagrams: pp. 147–163. Includes a description of Fortune's algorithm.
Rolf Klein (1989). Abstract voronoi diagrams and their applications. Lecture Notes in Computer Science 333. Springer-Verlag. pp. 148–157. doi:10.1007/3-540-50335-8_31. ISBN 3-540-52055-4.

External links

Wikimedia Commons has media related to Voronoi diagrams.

Tessellation

Periodic

Pythagorean Rhombille Schwarz triangle Rectangle Domino Uniform tiling & honeycomb Coloring Convex Kisrhombille Wallpaper group Wythoff

Aperiodic

Ammann–Beenker Aperiodic set of prototiles List Einstein problem Socolar–Taylor Gilbert Penrose Pentagonal Pinwheel Quaquaversal Rep-tile & Self-tiling Sphinx Truchet

Other

Anisohedral & Isohedral Architectonic & catoptric Circle Limit III Computer graphics Honeycomb Isotoxal Packing Problems Domino Wang Heesch's Squaring Prototile Conway criterion Girih Regular Division of the Plane Regular grid Substitution Voronoi Voderberg

By vertex type

Spherical	2ⁿ 3³.n V3³.n 4².n V4².n

Regular	2^∞ 3⁶ 4⁴ 6³

Semi- regular	3².4.3.4 V3².4.3.4 3³.4² 3³.∞ 3⁴.6 V3⁴.6 3.4.6.4 (3.6)² 3.12² 4².∞ 4.6.12 4.8²

Hyper- bolic	3².4.3.5 3².4.3.6 3².4.3.7 3².4.3.8 3².4.3.∞ 3².5.3.5 3².5.3.6 3².6.3.6 3².6.3.8 3².7.3.7 3².8.3.8 3³.4.3.4 3².∞.3.∞ 3⁴.7 3⁴.8 3⁴.∞ 3⁵.4 3⁷ 3⁸ 3^∞ (3.4)³ (3.4)⁴ 3.4.6².4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7)² (3.8)² 3.14² 3.16² (3.∞)² 3.∞² 4².5.4 4².6.4 4².7.4 4².8.4 4².∞.4 4⁵ 4⁶ 4⁷ 4⁸ 4^∞ (4.5)² (4.6)² 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7)² (4.8)² 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.10² 4.10.12 4.12² 4.12.16 4.14² 4.16² 4.∞² (4.∞)² 5⁴ 5⁵ 5⁶ 5^∞ 5.4.6.4 (5.6)² 5.8² 5.10² 5.12² (5.∞)² 6⁴ 6⁵ 6⁶ 6⁸ 6.4.8.4 (6.8)² 6.8² 6.10² 6.12² 6.16² 7³ 7⁴ 7⁷ 7.6² 7.8² 7.14² 8³ 8⁴ 8⁶ 8⁸ 8¹² 8.6² 8.16² ∞³ ∞⁴ ∞⁵ ∞^∞ ∞.6² ∞.8²

This article is issued from Wikipedia - version of the Thursday, February 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.