Dinitz conjecture
In combinatorics, the Dinitz conjecture is a statement about the extension of arrays to partial Latin squares, proposed in 1979 by Jeff Dinitz, and proved in 1994 by Fred Galvin.
The Dinitz conjecture, now a theorem, is that given an n × n square array, a set of m symbols with m ≥ n, and for each cell of the array an n-element set drawn from the pool of m symbols, it is possible to choose a way of labeling each cell with one of those elements in such a way that no row or column repeats a symbol.
The Dinitz conjecture is closely related to graph theory, in which it can be succinctly stated as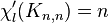 
for natural 
. It means that the list chromatic index of the complete bipartite graph 
equals . In fact, Fred Galvin proved the Dinitz conjecture as a special case of his theorem stating that the list chromatic index of any bipartite multigraph is equal to its chromatic index. Moreover, it is also a special case of the edge list coloring conjecture saying that the same holds not only for bipartite graphs, but also for any loopless multigraph.
References
- F. Galvin (1995). "The list chromatic index of a bipartite multigraph". Journal of Combinatorial Theory. Series B 63 (1): 153–158. doi:10.1006/jctb.1995.1011.
- Zeilberger, D. (1996). "The Method of Undetermined Generalization and Specialization Illustrated with Fred Galvin's Amazing Proof of the Dinitz Conjecture". The American mathematical monthly 103 (3): 233–239. arXiv:math/9506215.
- Chow, T. Y. (1995). "On the Dinitz conjecture and related conjectures". Discrete Math 145: 145–173. Retrieved 2009-04-15.