Differential graded algebra

In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.

Definition

A differential graded algebra (or simply DG-algebra) A is a graded algebra equipped with a map 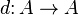$d\colon A \to A$ which is either degree 1 (cochain complex convention) or degree 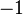$-1$ (chain complex convention) that satisfies two conditions:

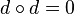$d \circ d=0$ .
This says that d gives A the structure of a chain complex or cochain complex (accordingly as the differential reduces or raises degree).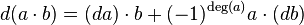
$d(a \cdot b)=(da) \cdot b + (-1)^{\operatorname{deg}(a)}a \cdot (db)$ , where deg is the degree of homogeneous elements.
This says that the differential d respects the graded Leibniz rule.

A more succinct way to state the same definition is to say that a DG-algebra is a monoid object in the monoidal category of chain complexes.

A differential graded augmented algebra (or simply DGA-algebra) or an augmented DG-algebra is a DG-algebra equipped with a morphism to the ground ring (the terminology is due to Henri Cartan).^[1]

Many sources use the term DGAlgebra for a DG-algebra.

Examples of DG-algebras

The Koszul complex is a DG-algebra.
The tensor algebra is a DG-algebra with differential similar to that of the Koszul complex.
The singular cohomology of a topological space with coefficients in Z/pZ is a DG-algebra: the differential is given by the Bockstein homomorphism associated to the short exact sequence 0 → Z/pZ → Z/p²Z → Z/pZ → 0, and the product is given by the cup product.
Differential forms on a manifold, together with the exterior derivation and the wedge product form a DG-algebra. See also de Rham cohomology.

Other facts about DG-algebras

The homology 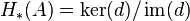$H_*(A) = \ker(d) / \operatorname{im}(d)$ of a DG-algebra 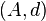$(A,d)$ is a graded algebra. The homology of a DGA-algebra is an augmented algebra.

References

↑ H. Cartan, Sur les groupes d'Eilenberg-Mac Lane H(Π,n), Proc. Nat. Acad. Sci. U. S. A. 40, (1954). 467–471

Manin, Yuri Ivanovich; Gelfand, Sergei I. (2003), Methods of Homological Algebra, Berlin, New York: Springer-Verlag, ISBN 978-3-540-43583-9 , see sections V.3 and V.5.6

This article is issued from Wikipedia - version of the Sunday, January 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Differential graded algebra

Definition

Examples of DG-algebras

Other facts about DG-algebras

See also

References