Desuspension

In topology, a field within mathematics, desuspension is an operation inverse to suspension.[1]

Definition

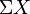In general, given an n-dimensional space X, the suspension \Sigma{X} has dimension n + 1. Thus, the operation of suspension creates a way of moving up in dimension. In the 1950s, to define a way of moving down, mathematicians introduced an inverse operation 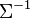\Sigma^{-1}, called desuspension.[2] Therefore, given an n-dimensional space X, the desuspension \Sigma^{-1}{X} has dimension n – 1.

Reasons

The reasons to introduce desuspension:

  1. Desuspension makes the category of spaces a triangulated category.
  2. If arbitrary coproducts were allowed, desuspension would result in all cohomology functors being representable.

See also

References

  1. ↑ Wolcott, Luke; McTernan, Elizabeth (2012). "Imagining Negative-Dimensional Space" (PDF). In Bosch, Robert; McKenna, Douglas; Sarhangi, Reza. Proceedings of Bridges 2012: Mathematics, Music, Art, Architecture, Culture. Phoenix, Arizona, USA: Tessellations Publishing. pp. 637–642. ISBN 978-1-938664-00-7. ISSN 1099-6702. Retrieved 25 June 2015.
  2. ↑ H. R. Margolis (1983). Spectra and the Steenrod Algebra. North-Holland. p. 454.

External links

This article is issued from Wikipedia - version of the Friday, August 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.