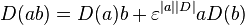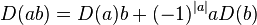Derivation (differential algebra)
In mathematics, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D : A → A that satisfies Leibniz's law:
More generally, if M is an A-bimodule, a K-linear map D : A → M that satisfies the Leibniz law is also called a derivation. The collection of all K-derivations of A to itself is denoted by DerK(A). The collection of K-derivations of A into an A-module M is denoted by DerK(A, M).
Derivations occur in many different contexts in diverse areas of mathematics. The partial derivative with respect to a variable is an R-derivation on the algebra of real-valued differentiable functions on Rn. The Lie derivative with respect to a vector field is an R-derivation on the algebra of differentiable functions on a differentiable manifold; more generally it is a derivation on the tensor algebra of a manifold. The Pincherle derivative is an example of a derivation in abstract algebra. If the algebra A is noncommutative, then the commutator with respect to an element of the algebra A defines a linear endomorphism of A to itself, which is a derivation over K. An algebra A equipped with a distinguished derivation d forms a differential algebra, and is itself a significant object of study in areas such as differential Galois theory.
Properties
The Leibniz law itself has a number of immediate consequences. Firstly, if x1, x2, ..., xn ∈ A, then it follows by mathematical induction that
(the last equality holds if, for all 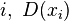 commutes with
commutes with 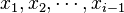 ).
).
In particular, if A is commutative and x1 = x2 = ... = xn, then this formula simplifies to the familiar power rule D(xn) = nxn−1D(x). Secondly, if A has a unit element 1, then D(1) = 0 since D(1) = D(1·1) = D(1) + D(1). Moreover, because D is K-linear, it follows that "the derivative of any constant function is zero"; more precisely, for any x ∈ K, D(x) = D(x·1) = x·D(1) = 0.
If k ⊂ K is a subring, and A is a k-algebra, then there is an inclusion
since any K-derivation is a fortiori a k-derivation.
The set of k-derivations from A to M, Derk(A, M) is a module over k. Furthermore, the k-module Derk(A) forms a Lie algebra with Lie bracket defined by the commutator:
It is readily verified that the Lie bracket of two derivations is again a derivation.
Graded derivations
Given a graded algebra A and a homogeneous linear map D of grade |D| on A, D is a homogeneous derivation if
for every homogeneous element a and every element b of A for a commutator factor ε = ±1. A graded derivation is sum of homogeneous derivations with the same ε.
If ε = 1, this definition reduces to the usual case. If ε = −1, however, then
for odd |D|, and D is called an anti-derivation.
Examples of anti-derivations include the exterior derivative and the interior product acting on differential forms.
Graded derivations of superalgebras (i.e. Z2-graded algebras) are often called superderivations.
See also
- In differential geometry derivations are tangent vectors
- Kähler differential
- Hasse derivative
- p-derivation
- Wirtinger derivatives
- Derivative of the exponential map
References
- Bourbaki, Nicolas (1989), Algebra I, Elements of mathematics, Springer-Verlag, ISBN 3-540-64243-9.
- Eisenbud, David (1999), Commutative algebra with a view toward algebraic geometry (3rd. ed.), Springer-Verlag, ISBN 978-0-387-94269-8.
- Matsumura, Hideyuki (1970), Commutative algebra, Mathematics lecture note series, W. A. Benjamin, ISBN 978-0-8053-7025-6.
- Kolař, Ivan; Slovák, Jan; Michor, Peter W. (1993), Natural operations in differential geometry, Springer-Verlag.
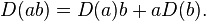
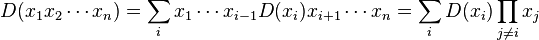
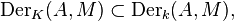
![[D_1,D_2] = D_1\circ D_2 - D_2\circ D_1.](../I/m/52a86cf13e6566d656d0daa5633111ff.png)