Dependence relation
In mathematics, a dependence relation is a binary relation which generalizes the relation of linear dependence.
Let  be a set. A (binary) relation
be a set. A (binary) relation 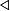 between an element
between an element  of
of  and a subset
and a subset  of
of  is called a dependence relation, written
is called a dependence relation, written 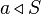 , if it satisfies the following properties:
, if it satisfies the following properties:
- if
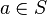 , then
, then 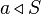 ;
; - if
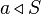 , then there is a finite subset
, then there is a finite subset  of
of  , such that
, such that 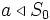 ;
; - if
 is a subset of
is a subset of  such that
such that 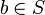 implies
implies 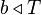 , then
, then 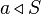 implies
implies 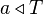 ;
; - if
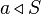 but
but 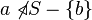 for some
for some 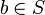 , then
, then 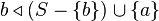 .
.
Given a dependence relation 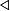 on
on  , a subset
, a subset  of
of  is said to be independent if
is said to be independent if 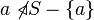 for all
for all 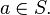 If
If 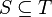 , then
, then  is said to span
is said to span  if
if 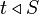 for every
for every 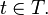
 is said to be a basis of
is said to be a basis of  if
if  is independent and
is independent and  spans
spans 
Remark. If  is a non-empty set with a dependence relation
is a non-empty set with a dependence relation 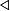 , then
, then  always has a basis with respect to
always has a basis with respect to 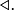 Furthermore, any two bases of
Furthermore, any two bases of  have the same cardinality.
have the same cardinality.
Examples
- Let
 be a vector space over a field
be a vector space over a field 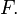 The relation
The relation 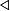 , defined by
, defined by 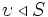 if
if 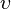 is in the subspace spanned by
is in the subspace spanned by  , is a dependence relation. This is equivalent to the definition of linear dependence.
, is a dependence relation. This is equivalent to the definition of linear dependence. - Let
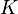 be a field extension of
be a field extension of 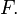 Define
Define 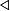 by
by 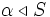 if
if  is algebraic over
is algebraic over 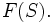 Then
Then 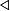 is a dependence relation. This is equivalent to the definition of algebraic dependence.
is a dependence relation. This is equivalent to the definition of algebraic dependence.
See also
This article incorporates material from Dependence relation on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.