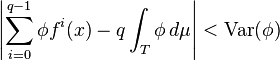Denjoy–Koksma inequality

In mathematics, the Denjoy–Koksma inequality, introduced by Herman (1979, p.73) as a combination of work of Arnaud Denjoy and the Koksma–Hlawka inequality of Jurjen Ferdinand Koksma, is a bound for Weyl sums 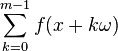$\sum_{k=0}^{m-1}f(x+k\omega)$ of functions f of bounded variation.

Statement

Suppose that a map f from the circle T to itself has irrational rotation number α, and p/q is a rational approximation to α with p and q coprime, |α – p/q| < 1/q². Suppose that φ is a function of bounded variation, and μ a probability measure on the circle invariant under f. Then

\left|\sum_{i=0}^{q-1} \phi f^i(x) - q\int_T \phi \, d\mu \right| < \operatorname{Var}(\phi)

(Herman 1979, p.73)

References

Herman, Michael-Robert (1979), "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations", Publications Mathématiques de l'IHÉS (49): 5–233, ISSN 1618-1913, MR 538680
Kuipers, L.; Niederreiter, H. (1974), Uniform distribution of sequences, New York: Wiley-Interscience [John Wiley & Sons], ISBN 978-0-486-45019-3, MR 0419394, Reprinted by Dover 2006

This article is issued from Wikipedia - version of the Sunday, July 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.