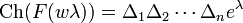Demazure module

In mathematics, a Demazure module, introduced by Demazure (1974a, 1974b), is a submodule of a finite-dimensional representation generated by an extremal weight space under the action of a Borel subalgebra. The Demazure character formula, introduced by Demazure (1974b, theorem 2), gives the characters of Demazure modules, and is a generalization of the Weyl character formula. The dimension of a Demazure module is a polynomial in the highest weight, called a Demazure polynomial.

Demazure modules

Suppose that g is a complex semisimple Lie algebra, with a Borel subalgebra b containing a Cartan subalgebra h. An irreducible finite-dimensional representation V of g splits as a sum of eigenspaces of h, and the highest weight space is 1-dimensional and is an eigenspace of b. The Weyl group W acts on the weights of V, and the conjugates wλ of the highest weight vector λ under this action are the extremal weights, whose weight spaces are all 1-dimensional.

A Demazure module is the b-submodule of V generated by the weight space of an extremal vector wλ, so the Demazure submodules of V are parametrized by the Weyl group W.

There are two extreme cases: if w is trivial the Demazure module is just 1-dimensional, and if w is the element of maximal length of W then the Demazure module is the whole of the irreducible representation V.

Demazure modules can be defined in a similar way for highest weight representations of Kac–Moody algebras, except that one now has 2 cases as one can consider the submodules generated by either the Borel subalgebra b or its opposite subalgebra. In the finite-dimensional these are exchanged by the longest element of the Weyl group, but this is no longer the case in infinite dimensions as there is no longest element.

Demazure character formula

History

The Demazure character formula was introduced by (Demazure 1974b, theorem 2). Victor Kac pointed out that Demazure's proof has a serious gap, as it depends on (Demazure 1974a, Proposition 11, section 2), which is false; see (Joseph 1985, section 4) for Kac's counterexample. Andersen (1985) gave a proof of Demazure's character formula using the work on the geometry of Schubert varieties by Ramanan & Ramanathan (1985) and Mehta & Ramanathan (1985). Joseph (1985) gave a proof for sufficiently large dominant highest weight modules using Lie algebra techniques. Kashiwara (1993) proved a refined version of the Demazure character formula that Littelmann (1995) conjectured (and proved in many cases).

Statement

The Demazure character formula is

\text{Ch}(F(w\lambda)) = \Delta_1\Delta_2\cdots\Delta_ne^\lambda

Here:

w is an element of the Weyl group, with reduced decomposition w = s₁...s_n as a product of reflections of simple roots.
λ is a lowest weight, and e^λ the corresponding element of the group ring of the weight lattice.
Ch(F(wλ)) is the character of the Demazure module F(wλ).
P is the weight lattice, and Z[P] is its group ring.
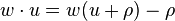$\rho$ is the sum of fundamental weights and the dot action is defined by $w\cdot u=w(u+\rho)-\rho$ .
Δ_α for α a root is the endomorphism of the Z-module Z[P] defined by

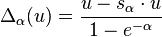
\Delta_\alpha(u) = \frac{u-s_\alpha \cdot u}{1-e^{-\alpha}}

and Δ_j is Δ_α for α the root of s_j

References

Andersen, H. H. (1985), "Schubert varieties and Demazure's character formula", Inventiones Mathematicae 79 (3): 611–618, doi:10.1007/BF01388527, ISSN 0020-9910, MR 782239
Demazure, Michel (1974a), "Désingularisation des variétés de Schubert généralisées", Annales Scientifiques de l'École Normale Supérieure. Quatrième Série, Collection of articles dedicated to Henri Cartan on the occasion of his 70th birthday, I 7: 53–88, ISSN 0012-9593, MR 0354697
Demazure, Michel (1974b), "Une nouvelle formule des caractères", Bulletin des Sciences Mathématiques. 2e Série 98 (3): 163–172, ISSN 0007-4497, MR 0430001
Joseph, Anthony (1985), "On the Demazure character formula", Annales Scientifiques de l'École Normale Supérieure. Quatrième Série 18 (3): 389–419, ISSN 0012-9593, MR 826100
Kashiwara, Masaki (1993), "The crystal base and Littelmann's refined Demazure character formula", Duke Mathematical Journal 71 (3): 839–858, doi:10.1215/S0012-7094-93-07131-1, ISSN 0012-7094, MR 1240605
Littelmann, Peter (1995), "Crystal graphs and Young tableaux", Journal of Algebra 175 (1): 65–87, doi:10.1006/jabr.1995.1175, ISSN 0021-8693, MR 1338967
Mehta, V. B.; Ramanathan, A. (1985), "Frobenius splitting and cohomology vanishing for Schubert varieties", Annals of Mathematics. Second Series 122 (1): 27–40, doi:10.2307/1971368, ISSN 0003-486X, MR 799251
Ramanan, S.; Ramanathan, A. (1985), "Projective normality of flag varieties and Schubert varieties", Inventiones Mathematicae 79 (2): 217–224, doi:10.1007/BF01388970, ISSN 0020-9910, MR 778124

This article is issued from Wikipedia - version of the Saturday, August 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.