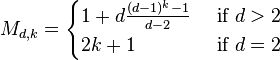Degree diameter problem
In graph theory, the degree diameter problem is the problem of finding the largest possible graph G (in terms of the size of its vertex set V) of diameter k such that the largest degree of any of the vertices in G is at most d. The size of G is bounded above by the Moore bound; for 1 < k and 2 < d only the Petersen graph, the Hoffman-Singleton graph, and maybe a graph of diameter k = 2 and degree d = 57 attain the Moore bound. In general the largest degree-diameter graphs are much smaller in size than the Moore bound.
Formula
Let 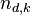 be the maximum possible of vertices for a graph with degree at most d and diameter k then
be the maximum possible of vertices for a graph with degree at most d and diameter k then 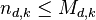 , where
, where 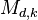 is the Moore bound:
is the Moore bound:
This bound is attained for very few graphs, thus the study moves to how close there exist graphs to the Moore bound.
For asymptotic behaviour note that 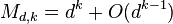 .
.
Define the parameter 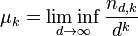 . It is conjectured that
. It is conjectured that 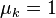 for all k. It is known that
for all k. It is known that 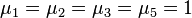 and that
and that 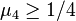 . For the general case it is known that
. For the general case it is known that 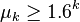 . Thus, although is conjectured that
. Thus, although is conjectured that 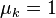 is still open if it is actually exponential.
is still open if it is actually exponential.
See also
- Cage (graph theory)
- Table of degree diameter graphs
- Table of vertex-symmetric degree diameter digraphs
- Maximum degree-and-diameter-bounded subgraph problem
References
- Bannai, E.; Ito, T. (1973), "On Moore graphs", J. Fac. Sci. Univ. Tokyo Ser. A 20: 191–208, MR 0323615
- Hoffman, Alan J.; Singleton, Robert R. (1960), "Moore graphs with diameter 2 and 3" (PDF), IBM Journal of Research and Development 5 (4): 497–504, doi:10.1147/rd.45.0497, MR 0140437
- Singleton, Robert R. (1968), "There is no irregular Moore graph", American Mathematical Monthly (Mathematical Association of America) 75 (1): 42–43, doi:10.2307/2315106, MR 0225679
- Miller, Mirka; Širáň, Jozef (2005), "Moore graphs and beyond: A survey of the degree/diameter problem", Electronic Journal of Combinatorics, Dynamic survey: DS14