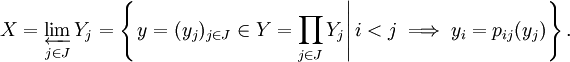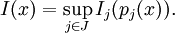Dawson–Gärtner theorem

In mathematics, the Dawson–Gärtner theorem is a result in large deviations theory. Heuristically speaking, the Dawson–Gärtner theorem allows one to transport a large deviation principle on a “smaller” topological space to a “larger” one.

Statement of the theorem

Let (Y_j)_j∈J be a projective system of Hausdorff topological spaces with maps p_ij : Y_j → Y_i. Let X be the projective limit (also known as the inverse limit) of the system (Y_j, p_ij)_i,j∈J, i.e.

X = \varprojlim_{j \in J} Y_{j} = \left\{ \left. y = (y_{j})_{j \in J} \in Y = \prod_{j \in J} Y_{j} \right| i < j \implies y_{i} = p_{ij} (y_{j}) \right\}.

Let (μ_ε)_ε>0 be a family of probability measures on X. Assume that, for each j ∈ J, the push-forward measures (p_j∗μ_ε)_ε>0 on Y_j satisfy the large deviation principle with good rate function I_j : Y_j → R ∪ {+∞}. Then the family (μ_ε)_ε>0 satisfies the large deviation principle on X with good rate function I : X → R ∪ {+∞} given by

I(x) = \sup_{j \in J} I_{j}(p_{j}(x)).

References

Dembo, Amir; Zeitouni, Ofer (1998). Large deviations techniques and applications. Applications of Mathematics (New York) 38 (Second ed.). New York: Springer-Verlag. pp. xvi+396. ISBN 0-387-98406-2. MR 1619036. (See theorem 4.6.1)

This article is issued from Wikipedia - version of the Wednesday, August 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.