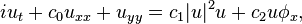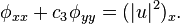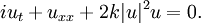Davey–Stewartson equation
In fluid dynamics, the Davey–Stewartson equation (DSE) was introduced in a paper by Davey & Stewartson (1974) to describe the evolution of a three-dimensional wave-packet on water of finite depth.
It is a system of partial differential equations for a complex (wave-amplitude) field 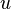 and a real (mean-flow) field
and a real (mean-flow) field  :
:
The DSE is an example of a soliton equation in 2+1 dimensions. The corresponding Lax representation for it is given in Boiti, Martina & Pempinelli (1995).
In 1+1 dimensions the DSE reduces to the nonlinear Schrödinger equation
Itself, the DSE is the particular reduction of the Zakharov–Schulman system. On the other hand, the equivalent counterpart of the DSE is the Ishimori equation.
The DSE is the result of a multiple-scale analysis of modulated nonlinear surface gravity waves, propagating over a horizontal sea bed.
See also
References
- Boiti, M.; Martina, L.; Pempinelli, F. (December 1995), "Multidimensional localized solitons", Chaos, Solitons & Fractals 5 (12): 2377–2417, Bibcode:1995CSF.....5.2377B, doi:10.1016/0960-0779(94)E0106-Y, ISSN 0960-0779, (subscription required (help))
- Davey, A.; Stewartson, K. (1974), "On three dimensional packets of surface waves", Proc. R. Soc. A 338 (1613): 101–110, Bibcode:1974RSPSA.338..101D, doi:10.1098/rspa.1974.0076
- Sattinger, David H.; Tracy, C. A.; Venakides, S., eds. (1991), Inverse Scattering and Applications, Contemporary Mathematics 122, Providence, RI: American Mathematical Society, ISBN 0-8218-5129-2, MR 1135850
External links
- Davey-Stewartson_system at the dispersive equations wiki.