Damage per second
Damage per second (DPS) is a term used with computer games to describe the average rate of damage inflicted over time. The term is especially common in massively multiplayer online role-playing games (MMORPG) and is a key aspect of theorycraft. In this circumstance, "Damage" is a scalar quantity that is applied to an in-game opponent, until that opponent's capacity for absorbing damage is exceeded and the opponent is defeated. Therefore, the higher the DPS value, the less time it takes to defeat an opponent.
The term can also be used as a verb - to "DPS" an opponent is to inflict the maximum damage possible in the shortest time or as a noun, to describe a class which has a particularly high DPS, though this usage is debatable, with "DD" (Damage Dealer) an acceptable alternative.
Usefulness
As a measure of capability, it is more accurate than a simple damage value that does not reflect how often the damage can be dealt. In Eve Online, the players' weapons fire in volleys, while in more traditional MMOs the player strikes with melee weapons or fire ranged weapons or spells, which may need to 'recharge'. While an attack may deal 500 points of damage, if the weapon can only fire once every 5 seconds, the damage will be calculated as 100 damage per second. It is therefore a useful metric both to game players and game designers.
DPS formula / attack chains
There are certain aspects of the actual attacks a player must know in order to calculate a DPS Attack Chain. The following three attributes are generally regarded as universal throughout the MMO community:
- Base Damage: The damage an attack does regardless of equipped gear or outside enhancements.
- Base Recharge/Cool down: The time it takes for the attack to be used again.
- Activation Time: The time it takes for an attack to animate.
Tying these together is the simple formula of: Damage / (Activation Time + Recharge) = Damage per Second
As an example, if a player has an attack that does 75 damage, with an activation time of .25 seconds and a recharge of .75 seconds, the DPS is calculated as:
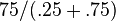
|
Using this attack, the character can apply 75 damage every second indefinitely, barring game restrictions such as energy or ammunition, to their target. However, most of the time one attack simply is not enough to yield significant DPS to bring down a tough foe. For this, it is necessary to calculate the DPS of a series of attacks. To do so, the calculation is performed disregarding the recharge.
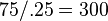 Damage per Activation. Damage per Activation. |
What this means is that the original attack has the potential to do 300 damage in a second, as with only its activation time as a limit for how often the base damage can be applied within the time period. An attack's DPA is more important than its individual DPS, as by the time the player activates another attack, their first attack may be recharged already, making the recharge part of the equation redundant.
Adding a second attack to a character, such as a slower but more damaging attack: 100 damage, activation time of .50 seconds and a recharge of .75 seconds.
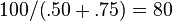 DPS DPS
|
The fact that an attack does more base damage does not necessarily mean that it would be good for an attack chain, which varies per chain. As for making the chain, it's convenient to use small intervals in time like .25 seconds (the greatest common divisor of the activation and recharge times) and put them in a table: (let's assume we start with attack 1)
| Attack | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | R | R | R | - | A | R | R | R | - |
| 2 | - | A | A | R | R | R | A | A | R | R |
| Result | A | A | A | - | - | A | A | A | - | - |
Where A denotes an Activation interval and R a Recharge interval. Notice that there is a returning pattern called a cycle, with length 5 short intervals of 0.25. In such a cycle there are 3 intervals occupied with Activation and two empty intervals (see also Get a filler attack).
With this starting point, we can now figure out the "long-term DPS" of these attacks. For convenience, they both have a recharge of .75 seconds. Why recharge is important again is due to the player wanting to recycle the first attack, as it has the high DPA number needed to get high DPS. We'll now calculate the DPS for such a cycle:
Damage per cycle: 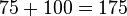 damage damage
Time per cycle: DPS for the cycle: |
From this point the first attack will have recharged, and the cycle is essentially complete, giving us 140 DPS overall. To increase DPS, and avoid the down time created by the recharge times, one can do two things:
- Get a filler attack: A “filler” is an attack which can be inserted into a string that may have non-optimal DPA, but its recharge and activation times may be just enough to prevent the gap seen above as the character waits for one of its two attacks to recharge. This keeps the character continuously dealing damage and as a result deals higher DPS.
- Reduce the Recharge/Increase the Damage: A second option available for all characters in an MMO is to “buff” their attacks (granted they lack a filler) via equipping certain gear, items or by casting certain spells on themselves for a time. By increasing the damage, or decreasing the recharge time (optimally both), a player can attain much higher DPS as their best chain now does more damage without pauses.
To fit these examples into our chain, say there was an attack that perfectly fit the recharge “gap” created by our first two attacks, and did 50 damage. Our chain would now follow a repeating 1-2-3 pattern, and have a sustained 180 DPS, which is a nice improvement to the old chain. If the damage and recharge times of the two attacks were to each be buffed by say, 25% (x 1.25 for damage, / 1.25 for recharge), they would have the following attributes: 93.75 and 125 damage, .6 seconds recharge.
Recalculating the chain, we get 218.75 damage in a cycle of length 1.10, resulting in 198.86 DPS compared to 140, also an interesting boost. Notice that there still is a 'hole' of 0.35 seconds of free time in the enhanced cycle, so combining the right enhancements with a (buffed) filler attack will give an even greater DPS.
Other variables
Aside from the standard trio of factors, there exist other variables that can add or subtract effectiveness from a character's attack chain.
The following affect the player directly:
- Critical Hit / Glancing Blow: These types of strikes emulate hitting vital or well armored sections of a target, doing additional or reduced damage, respectively. How these would be calculated would be to figure out the chances of each happening, then apply the number to the total damage. For example, a player has a 10% chance to critically hit for double damage, and a 5% chance to do a Glancing Blow for half damage. Right away they can simply subtract the GB from the CR as they cancel each other out if they are in equal occurrence, then simply multiply the final damage by 5% (1.05), or (0.95) if the opposite is true.
- (Self) Buffs: Similar to enhancing a character with gear, items or spells, a buff cast upon the player's own character can give them temporary boosts to their abilities before starting a battle. To calculate, simply add its value as described above: Base Damage (1.00 + Enhancement + Buff). For example, an attack with a base damage of 100, an enhancement of 50%, and a buff of 10% would be now doing 160 damage (100 x 1.6).
- Enemy De-buffs: De-buffing an enemy is essentially the same as when the player is buffed, but in a negative manner. Calculating it is the same as calculating a buff. For example, a spell that makes a target receive 10% more damage from attacks. Calculating this is exactly the same as having a 10% buff to a character's damage directly. However, the enemy with the 10% debuff may also be targeted by allies of the attacker, taking more damage for the duration of the debuff overall.
The following affect the player indirectly:
- Enemy Resistance/Defense: Resistance (or Defense) affects how much damage a given target receives from attacks. For example, an enemy has 50% resistance to fire-based attacks, hitting it with a fire-based attack sub sequentially will do half the damage, effectively cutting an attacker's DPS in half if they rely on fire attacks. This can be worked around by using different attacks in the chain, or by de-buffing the enemy's resistance with a spell.
- Enemy Healing/Regeneration: An enemy that can heal itself can render a player's DPS highly ineffective if not useless, as it is countering Damage per Second with Healing per Second. To beat this, a player simply needs to out-DPS their HPS. Failure to do so mean that it is statistically impossible for said player to beat that enemy. However, some characters have the ability to de-buff enemy healing or regeneration, making the task much easier.
- Range / Movement: All attacks have a set range from point-blank melee attacks, to long ranged assaults. Also, most all characters whether player or enemy have the ability to move about their terrain. Keeping in mind the range of some moves during combat could make or break an attack chain as the attacker or enemy may be too close or too far away by just the right amount to make an attack not activate, and reduce the DPS. This indirectly affects the player as “Enemy AI” dictates how they may move around and skew with certain attacks in a player's arsenal.
Another key factor may be Accuracy (chance of an attack to hit a target), but for most calculations it is assumed the attacks will be hitting. However, realistically most characters in most MMO's need to somehow ensure they hit their intended targets, and most likely will enhance accuracy on their characters, sometimes sacrificing recharge enhancements and the like. This cuts down on theoretical DPS, but increases realistic values as they actually land every hit of their attack chain.
Other calculation method
In some games there are certain bosses that have a set amount of health, with little or no other variables other than their (usually high) amount of health. Players often then simply use their attack chains against them, and time how long it takes to deplete the boss's health. For example, if the boss has 10,000 health, and it takes a player 50 seconds to defeat the boss, the player's attack chain does 200 DPS. These fights are often known as "tank-and-spank" fights. They may alternatively be known as a "Patchwerk" fight, after the World of Warcraft boss encounter of the same name. This encounter was often used as a gauge of individual or group DPS due to the tight enrage timer and the lack of secondary encounter mechanics requiring the attention or reaction of damage-dealers.
Sustainable DPS
While some bosses have a strategy, often this strategy can be escaped or overcome through alternative means unintended by the developers. One is the burn-down (some bosses are actually designed this way). The other way is being able to withstand a boss's attacks and continue to produce damage indefinitely. In general, sustainable DPS refers to the ability to produce damage over a long period of time through their attack chain. In a raid specifically, this refers to the ability to stand and fight however long it takes until the boss is defeated.
Achieving sustainable DPS in a boss fight can be challenging; energy/mana, consumables, ammo and chaos control can all be serious barriers to the ability to stage a long-term fight. Raid bosses also often cull inattentive players, making extended vigilance a problem as well. Since the burn-down fights are faster and more convenient, they are often preferred, saving sustainable DPS as a last resort.
However, this method allows a specially geared and prepared raid group to face bosses with very high health values, making it a valuable tool in the raider's arsenal.
Variations
Some create variations and laws on the idea of damage per second. One such is the countering force of healing, or healing per second, denoted as "HPS". One law that describes the effects of Healing and Damaging on a single target is known as the "Law of healing damage equivalence" which goes off the fact that the idea of healing is equal but opposite to the idea of damaging, otherwise, [H=-D] where "H" is healing and "D" is damage. The before-mentioned law states "If the sum of one or more damaging sources is equivalent to the sum of one or more healing sources then the total net damage will be equal to zero. Assuming both sources occur within the product of each time." Which means that when the total net healing is equal to the total net damaging within the same time interval, the damage taken is zero. It is described in the formula: [Hnet = Dnet then Dt = 0] where Dt is total damage taken, Hnet is total healing done and Dnet is total damage done.

 Damage over 1 second (75 DPS)
Damage over 1 second (75 DPS) Damage per Activation
Damage per Activation seconds
seconds DPS
DPS