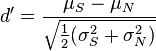Sensitivity index
The sensitivity index or d' (pronounced 'dee-prime') is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, compared against the standard deviation of the signal plus noise distributions. For normally distributed signal and noise with mean and standard deviations 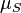 and
and 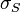 , and
, and 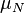 and
and 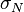 , respectively, d' is defined as:
, respectively, d' is defined as:
An estimate of d' can be also found from measurements of the hit rate and false-alarm rate. It is calculated as:
- d' = Z(hit rate) − Z(false alarm rate),[2]
where function Z(p), p ∈ [0,1], is the inverse of the cumulative distribution function of the Gaussian distribution.
d' is a dimensionless statistic. A higher d' indicates that the signal can be more readily detected.
See also
References
- ↑ Samuel Gale and David Perkel. A Basal Ganglia Pathway Drives Selective Auditory Responses in Songbird Dopaminergic Neurons via Disinhibition. The Journal of Neuroscience (2010). 30(3):1027–1037
- ↑ MacMillan N, Creelman C (2005) Detection Theory: A User’s Guide. Lawrence Erlbaum Associates. (p. 7)
- Wickens, Thomas D. (2001) Elementary Signal Detection Theory, OUP USA. ISBN 0-19-509250-3 (Ch. 2, p. 20). Excerpts
External links
- Interactive signal detection theory tutorial including calculation of d'.
This article is issued from Wikipedia - version of the Wednesday, December 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.