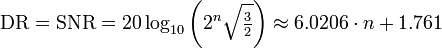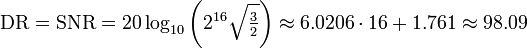dBFS

Clipping of a digital waveform

Decibels relative to full scale, commonly abbreviated dBFS, measures decibel amplitude levels in digital systems such as pulse-code modulation (PCM) which have a defined maximum available peak level.

0 dBFS is assigned to the maximum possible digital level.^[1] For example, a signal that reaches 50% of the maximum level at any point would reach −6 dBFS at that point, 6 dB below full scale. Conventions differ for RMS measurements, but all peak measurements will be negative numbers, unless they reach the maximum digital value.

A digital signal which does not contain any samples at 0 dBFS can still clip when converted to analog due to the signal reconstruction process interpolating between samples. This possibility can be prevented by careful digital-to-analog converter circuit design.^[2]

RMS levels

Since a peak measurement is not useful for qualifying the noise performance of a system, or measuring the loudness of an audio recording, for instance, RMS measurements are often used instead.

There is a potential for ambiguity when assigning a level on the dBFS scale to a waveform rather than to a specific amplitude, since some choose the reference level so that RMS and peak measurements of a sine wave produce the same number, while others want the RMS and peak values of a square wave to be equal, as they are in typical analog measurements.^[3][4][5]

• RMS: For the case in which the RMS value of a full-scale square wave is designated 0 dBFS, all possible dBFS measurements are negative numbers. A sine wave could not exist at a larger RMS value than −3 dBFS without clipping, by this convention.^[6] This is the convention used in Euphonix meters.^[7]
• Peak: For the case in which the RMS value of a full-scale sine wave is designated 0 dBFS, a full-scale square wave would have an RMS of +3 dBFS.^[8][9] This is the definition specified in AES Standard AES17-1998^[10] and IEC 61606 and used in Dorrough meters,^[7] Analog Devices^[11] and Wolfson^[12] digital microphone specs, etc.

Dynamic range

The measured dynamic range of a digital system is the ratio of the full scale signal level to the RMS noise floor. The theoretical minimum noise floor is caused by quantization noise. This is usually modeled as a uniform random fluctuation between −1/2 LSB and +1/2 LSB. (Only certain signals produce uniform random fluctuations, so this model is typically, but not always, accurate.)^[13]

As the dynamic range is measured relative to the RMS level of a full scale sine wave, the dynamic range and the level of this quantization noise in dBFS can both be estimated with the same formula (though with reversed sign):

The value of n equals the resolution of the system in bits or the resolution of the system minus 1 bit (the measure error). For example, a 16-bit system will have a theoretical minimum noise floor of -98.09 dBFS relative to a full-scale sine wave:

In any real converter, dither is added to the signal before sampling. This removes the effects of non-uniform quantization error, but increases the minimum noise floor.

Notes

Although the decibel (dB) is permitted for use alongside SI units, the dBFS is not.^[14]

The term dBFS was first coined in the early 1980s by James Colotti, an analog engineer who pioneered some of the dynamic evaluation techniques of high-speed A/D and D/A Converters. Mr. Colotti first introduced the term to industry at the RF Expo East in Boston Massachusetts in November 1987, during his presentation “Digital Dynamic Analysis of A/D Conversion Systems through Evaluation Software based on FFT/DFT Analysis".

Analog levels

dBFS is not to be used for analog levels, according to AES-6id-2006. There is no single standard for converting between digital and analog levels, mostly due to the differing capabilities of different equipment. The amount of oversampling also affects the conversion with values that are too low having significant error. The conversion level is chosen as the best compromise for the typical headroom and signal-to-noise levels of the equipment in question. Examples:^[15][16][17]

• EBU R68 is used in most European countries, specifying +18 dBu at 0 dBFS
• In Europe, the EBU recommend that -18 dBFS equates to the Alignment Level
• European & UK calibration for Post & Film is −18 dBFS = 0 VU
• UK broadcasters, Alignment Level is taken as 0 dBu (PPM4 or -4VU)
• US installations use +24 dBu for 0 dBFS
• American and Australian Post: −20 dBFS = 0 VU = +4 dBu
• The American SMPTE standard defines -20 dBFS as the Alignment Level
• In Japan, France and some other countries, converters may be calibrated for +22 dBu at 0 dBFS.
• BBC spec: −18 dBFS = PPM "4" = 0 dBu
• German ARD & studio PPM +6 dBu = −10 (−9) dBFS. +16 (+15)dBu = 0 dBFS. No VU.
• Belgium VRT: 0dB (VRT Ref.) = +6dBu ; -9dBFS = 0dB (VRT Ref.) ; 0dBFS = +15dBu.
• ITU (telephony standards): In G.100.1 dBov (another term for dBFS) cannot exceed -3.01 dBov when measuring a tone played at maximum level

See also

• Audio bit depth
• Bit rate
• Full scale

References

External links

• Rane pro audio reference definition of dBFS
• dBFS – Sweetwater glossary