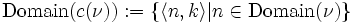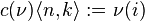Cylindrification
In computability theory a cylindrification is a construction that associates a cylindric numbering to each numbering. The concept was first introduced by Yuri L. Ershov in 1973.
Definition
Given a numbering 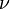 the cylindrification
the cylindrification 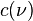 is defined as
is defined as
where 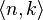 is the Cantor pairing function.
The cylindrification operation takes a relation as input of arity k and outputs a relation of arity k + 1 as follows : Given a relation R of arity K, its cylindrification denoted by c(R), is the following set {(a1,...,ak,a)|(a1,...,ak)belongs to R and a belongs to A}. Note that the cylindrification operation increases the arity of an input by 1.
is the Cantor pairing function.
The cylindrification operation takes a relation as input of arity k and outputs a relation of arity k + 1 as follows : Given a relation R of arity K, its cylindrification denoted by c(R), is the following set {(a1,...,ak,a)|(a1,...,ak)belongs to R and a belongs to A}. Note that the cylindrification operation increases the arity of an input by 1.
Properties
- Given two numberings
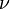 and
and 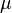 then
then 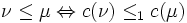
-
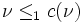
References
- Yu. L. Ershov, "Theorie der Numerierungen I." Zeitschrift für mathematische Logik und Grundlagen der Mathematik 19, 289-388 (1973).
This article is issued from Wikipedia - version of the Monday, December 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.