Cyclotomic unit

In mathematics, a cyclotomic unit (or circular unit) is a unit of an algebraic number field which is the product of numbers of the form (ζa
n − 1) for ζ
n an n^th root of unity and 0 < a < n. Note that if n is the power of a prime ζa
n − 1 itself is not a unit; however the numbers (ζa
n − 1)/(ζ
n − 1) for (a, n) = 1, and ±ζa
n generate the group of cyclotomic units in this case (n power of a prime).

The cyclotomic units form a subgroup of finite index in the group of units of a cyclotomic field. The index of this subgroup of real cyclotomic units (those cyclotomic units in the maximal real subfield) within the full unit group is equal to the class number of the maximal real subfield of the cyclotomic field.^[1]

Note also that if n is a composite number, the subgroup of cyclotomic units generated by (ζa
n − 1)/(ζ
n − 1)with (a, n) = 1 is not of finite index in general.^[2]

The cyclotomic units satisfy distribution relations. Let a be a rational number prime to p and let g_a denote exp(2πia)−1. Then for a≠ 0 we have 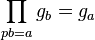.^[3]

Using these distribution relations and the symmetry relation ζa
n − 1 = -ζa
n (ζ-a
n − 1) a basis B_n of the cyclotomic units can be constructed with the property that B_d ⊆ B_n for d | n.^[4]

See also

• Elliptic unit
• Modular unit

References

• Lang, Serge (1990). Cyclotomic Fields I and II. Graduate Texts in Mathematics 121 (second combined ed.). Springer Verlag. ISBN 3-540-96671-4. Zbl 0704.11038. 
• Narkiewicz, Władysław (1990). Elementary and analytic theory of numbers (Second, substantially revised and extended ed.). Springer-Verlag. ISBN 3-540-51250-0. Zbl 0717.11045. 
• Washington, Lawrence C. (1997). Introduction to Cyclotomic Fields. Graduate Texts in Mathematics 83 (2nd ed.). Springer-Verlag. ISBN 0-387-94762-0. Zbl 0966.11047.