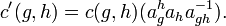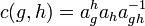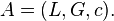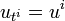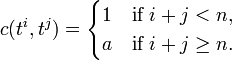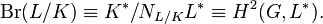Factor system

In mathematics, a factor system is a function on a group giving the data required to construct an algebra. A factor system constitutes a realisation of the cocycles in the second cohomology group in group cohomology.

Let G be a group and L a field on which G acts as automorphisms. A cocycle or factor system is a map c:G × G → L^* satisfying

c(h,k)^g c(hk,g) = c(h,kg) c(k,g) .

Cocycles are equivalent if there exists some system of elements a : G → L^* with

c'(g,h) = c(g,h) (a_g^h a_h a_{gh}^{-1}) .

Cocycles of the form

c(g,h) = a_g^h a_h a_{gh}^{-1}

are called split. Cocycles under multiplication modulo split cocycles form a group, the second cohomology group H²(G,L^*).

Crossed product algebras

Let us take the case that G is the Galois group of a field extension L/K. A factor system c in H²(G,L^*) gives rise to a crossed product algebra A, which is a K-algebra containing L as a subfield, generated by the elements λ in L and u_g with multiplication

\lambda u_g = u_g \lambda^g ,

u_g u_h = u_{gh} c(g,h) .

Equivalent factor systems correspond to a change of basis in A over K. We may write

A = (L,G,c) .

Every central simple algebra over K that splits over L arises in this way.^[1] The tensor product of algebras corresponds to multiplication of the corresponding elements in H². We thus obtain an identification of the Brauer group, where the elements are classes of CSAs over K, with H².^[2]^[3]

Cyclic algebra

Let us further restrict to the case that L/K is cyclic with Galois group G of order n generated by t. Let A be a crossed product (L,G,c) with factor set c. Let u = u_t be the generator in A corresponding to t. We can define the other generators

u_{t^i} = u^i \,

and then we have uⁿ = a in K. This element a specifies a cocycle c by

c(t^i,t^j) = \begin{cases} 1 & \text{if } i+j < n, \\ a & \text{if } i+j \ge n. \end{cases}

It thus makes sense to denote A simply by (L,t,a). However a is not uniquely specified by A since we can multiply u by any element λ of L^* and then a is multiplied by the product of the conjugates of λ. Hence A corresponds to an element of the norm residue group K^*/N_L/KL^*. We obtain the isomorphisms

\operatorname{Br}(L/K) \equiv K^*/N_{L/K} L^* \equiv H^2(G,L^*) .

References

↑ Jacobson (1996) p.57
↑ Saltman (1999) p.44
↑ Jacobson (1996) p.59

Lorenz, Falko (2008). Algebra. Volume II: Fields with Structure, Algebras and Advanced Topics. Universitext. Translated from the German by Silvio Levy. With the collaboration of the translator. Springer-Verlag. ISBN 978-0-387-72487-4. Zbl 1130.12001.
Jacobson, Nathan (1996). Finite-dimensional division algebras over fields. Berlin: Springer-Verlag. ISBN 3-540-57029-2. Zbl 0874.16002.
Reiner, I. (2003). Maximal Orders. London Mathematical Society Monographs. New Series 28. Oxford University Press. ISBN 0-19-852673-3. Zbl 1024.16008.
Saltman, David J. (1999). Lectures on division algebras. Regional Conference Series in Mathematics 94. Providence, RI: American Mathematical Society. ISBN 0-8218-0979-2. Zbl 0934.16013.

This article is issued from Wikipedia - version of the Saturday, July 05, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.