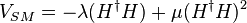Custodial symmetry

In particle physics the extra symmetry of the Higgs potential in the Standard Model

V_{SM} = -\lambda (H^\dagger H) + \mu(H^\dagger H)^2

responsible for keeping \rho ≈ 1 and insuring small corrections to \rho is called a custodial symmetry.[1] (Note \rho is a ratio involving the masses of the weak bosons and the Weinberg angle).

With one or more electroweak Higgs doublets in the Higgs sector, the effective action term 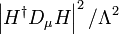\left|H^\dagger D_\mu H\right|^2/\Lambda^2 which generically arises whenever we have new physics beyond the Standard Model at the scale Λ contributes to the Peskin-Takeuchi T parameter. However, current precision electroweak measurements restrict Λ to more than a few TeV. This will not be a problem if we have no new physics right up to at least that scale. However, attempts to solve the gauge hierarchy problem generically require the addition of new particles below that scale. The preferred way of preventing the nasty 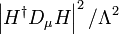\left|H^\dagger D_\mu H\right|^2/\Lambda^2 term from being generated is to introduce an approximate symmetry which acts upon the Higgs sector. In addition to the gauged SU(2)W which acts exactly upon the Higgs doublets, we will also introduce another approximate global SU(2)R symmetry which also acts upon the Higgs doublet. The Higgs doublet is now a real representation (2,2) of SU(2)L × SU(2)R with four real components. Here, we have relabeled W as L following the standard convention. Such a symmetry will not forbid Higgs kinetic terms like 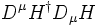D^\mu H^\dagger D_\mu H or tachyonic mass terms like 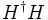H^\dagger H or self-coupling terms like 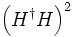\left(H^\dagger H\right)^2 (fortunately!) but will outlaw 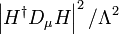\left|H^\dagger D_\mu H\right|^2/\Lambda^2. On the other hand, such an SU(2)R symmetry can never be exact and unbroken because otherwise, the up-type and the down-type Yukawa couplings will be exactly identical. Besides, SU(2)R does not map the hypercharge symmetry U(1)Y to itself but this is not too much of a problem because the hypercharge gauge coupling strength is small and in the limit as it goes to zero, we won't have a problem. In the parlance of model building, we say that U(1)Y is weakly gauged and this explicitly breaks SU(2)R. After the Higgs doublet acquires a nonzero vacuum expectation value, the (approximate) SU(2)L × SU(2)R symmetry is spontaneously broken to the (approximate) diagonal subgroup SU(2)V. This approximate symmetry is called the custodial symmetry.[2]

See also

References

  1. ↑ P. Sikivie, L. Susskind, M. B. Voloshin and V. I. Zakharov, Nucl. Phys. B 173, 189 (1980).
  2. ↑ B. Grzadkowski, M. Maniatis, Jose Wudka, "Note on Custodial Symmetry in the Two-Higgs-Doublet Model", arXiv:1011.5228.

External links

This article is issued from Wikipedia - version of the Friday, November 07, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.