Cross-polarized wave generation

Fig. 1.

Cross polarized wave (XPW) generation is a nonlinear optical process that can be classified in the group of frequency degenerate [four wave mixing] processes. It can take place only in media with anisotropy of third order nonlinearity. As a result of such nonlinear optical interaction at the output of the nonlinear crystal it is generated a new linearly polarized wave at the same frequency, but with polarization oriented perpendicularly to the polarization of input wave

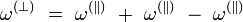$\omega^{(\perp)}~=~\omega^{(\|)}~+~\omega^{(\|)}~-~\omega^{(\|)}$ .

Simplified optical scheme for XPW generation is shown on Fig. 1. It consists of a nonlinear crystal plate (thick 1-2 mm) sandwiched between two crossed polarizers. The intensity of generated XPW has cubic dependence with respect to the intensity of the input wave. In fact this is the main reason this effect is so successful for improvement of the contrast of the temporal and spatial profiles of femtosecond pulses. Since cubic crystals are used as nonlinear media they are isotropic with respect to linear properties (there is no birefringence) and because of that the phase and group velocities of both waves XPW and the fundamental wave(FW) are equal:V_XPW=V_FW and V_gr,XPW=V_gr,FW. Consequence of that is ideal phase and group velocity matching for the two waves propagating along the crystal. This property allows obtaining very good efficiency of the XPW generation process with minimum distortions of the pulse shape and the spectrum.

Description of the process

Let us consider the case of interaction of two perpendicularly polarized waves in nonlinear media with cubic nonlinearity [1]. The equations describing the self phase modulation of the fundamental wave A and the generation of new wave perpendicularly polarized wave B in condition that |B| << |A| (i.e. when the depletion of the fundamental wave is neglected, self and cross phase modulation of wave B) can be written in following form:

Fig. 2. Dependence of the efficiency of XPW generation for three different time and spatial profiles: rectangular (top hat) in space and Gaussian in time (gray solid line); Gaussian in time and space (dash line); rectangular in time and space, i. e. plane wave (black solid line).

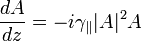\frac{d A}{dz} =-i \gamma_{\|}|A|^2A

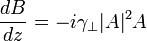\frac{d B}{dz} =-i \gamma_{\perp}|A|^2A

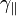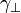where $\gamma_{\|}$ and $\gamma_{\perp}$ are coefficients that depend on (i) the orientation of the sample with respect to the crystal axes (see [3] for the expressions for two popular orientations: Z-cut and for holographic cut); (ii) the component 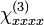$\chi^{(3)}_{xxxx}$ and (iii) anisotropy of 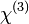$\chi^{(3)}_{}$ tensor.

The solution of this simplified system with initial conditions А(0)=А₀ and B (0) = 0 is:

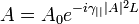A = A_0 e^{-i \gamma_{||} |A|^2L}

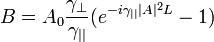B = A_0 \frac{\gamma_{\perp}}{\gamma_{||}}(e^{-i \gamma_{||} |A|^2L}-1)

where L is the length of the nonlinear media. In case of CW pump, the efficiency $\eta$ , that is defined as ratio of XPW intensity I_out at the output of the nonlinear media to the intensity of the input wave I_in can be described by sin² function of input intensity × length product:

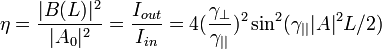(1) $\eta=\frac{|B(L)|^2}{|A_0|^2}=\frac{I_{out}}{I_{in}} =4(\frac{\gamma_{\perp}}{\gamma_{||}})^2 \sin^2(\gamma_{||} |A|^2L/2)$ .

If self phase modulation is relatively small 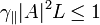$\gamma_{\|} |A|^{2}L \leq 1$ then:

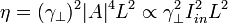(2) $\eta =({\gamma_{\perp}})^2 |A|^4L^2 \propto \gamma_{\perp}^2I_{in}^2L^2$ .

Fig. 3. Experimentally measured XPW generation efficiency as a function of input energy (in μJ) with use of BaF2 crystal(s) for one crystal scheme (upper plot) and two crystal scheme (lower plot).

The last expression (2) indicates that when nonlinear phase shift of the fundamental wave 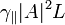$\gamma_{\|} |A|^{2}L$ is relatively small the efficiency grows as square of input intensity. The increase of the nonlinear phase shift above 3 prevents the coherent growing of XPW signal and leads in principle to periodical dependence of the efficiency as a function of input intensity. The use of two crystal scheme [2,3] allows this problem to be overcome.

Accounting the temporal and spatial shapes leads to reduction of the predicted by expression (1) efficiency. This is illustrated on Fig. 2 where the exact solution with all processes accompanying the effect of generation of XPW taken into account is given. The maximum XPW efficiency obtained with single crystal scheme approaches 12% for Gaussian in space and in time, while for top-hat spatial profile and Gaussian in time the maximum achieved efficiency is 29%. This behavior is direct consequence of the nonlinearity of the process. Typical experimental results for generation of XPW in BaF2 crystal are shown in Fig. 3. It is seen the efficiency of XPW process in single crystal scheme saturates close to 10%, while with two crystal scheme one can achieve 20–30% efficiency for XPW generation [2,3].

The effect of XPW generation is finding application for enhancement of the temporal contrast of femtosecond pulses [4] and for their monitoring and control. The approach of XPW generation for cleaning femtosecond pulses will be used in the Extreme Light Infrastructure European project.

For additional reading

[1] N. Minkovski et al., Opt. Lett., vol. 27, pp. 2025–2027 (2002); N. Minkovski et al., J. Opt. Soc. Am. B, vol. 21, pp. 1659–1664 (2004).

[2] A. Jullien et al., Opt. Express, vol. 14, pp. 2760–2769 (2006); A. Jullien et al., Appl. Phys. B, vol. 84, pp. 409–414 (2006).

[3] L. Canova et al., Appl. Phys. Lett., vol. 92, pp. 231102_1-3 (2008).

[4] A. Jullien et al.,Opt. Lett., vol. 30, pp.920–922 (2005); V. Chvykov et al., Opt. Lett., vol. 31, pp. 1456–1458 (2006).

This article is issued from Wikipedia - version of the Monday, October 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.