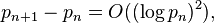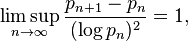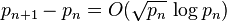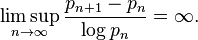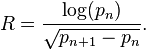Cramér's conjecture

In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936,^[1] is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that

p_{n+1}-p_{n}=O((\log p_{n})^{2}),\

where p_n denotes the nth prime number, O is big O notation, and "log" is the natural logarithm. While this is the statement explicitly conjectured by Cramér, his argument actually supports the stronger statement

\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{(\log p_{n})^{2}}}=1,

and this formulation is often called Cramér's conjecture in the literature.

Neither form of Cramér's conjecture has yet been proven or disproven.

Conditional proven results on prime gaps

Cramér gave a conditional proof of the much weaker statement that

p_{n+1}-p_{n}=O({\sqrt {p_{n}}}\,\log p_{n})

on the assumption of the Riemann hypothesis.^[1]

In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,^[2]

\limsup _{n\to \infty }{\frac {p_{n+1}-p_{n}}{\log p_{n}}}=\infty .

Heuristic justification

Cramér's conjecture is based on a probabilistic model (essentially a heuristic) of the primes, in which one assumes that the probability of a natural number of size x being prime is 1/log x. This is known as the Cramér model of the primes. Cramér proved that in this model, the above conjecture holds true with probability one.^[1]

Related conjectures and heuristics

Prime gap function

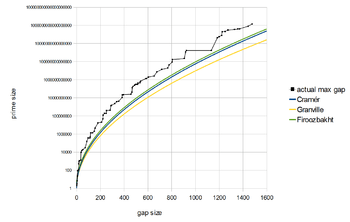
Daniel Shanks conjectured asymptotic equality of record gaps, a somewhat stronger statement than Cramér's conjecture.^[3]

In the Cramér random model,

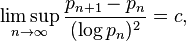\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{(\log p_{n})^{2}}}=c,

with

c=1.

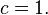
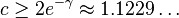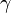However, as pointed out by Andrew Granville,^[4] Maier's theorem shows that the Cramér random model does not adequately describe the distribution of primes, and a refinement of Cramér's model taking into account divisibility by small primes suggests that $c\geq 2e^{-\gamma }\approx 1.1229\ldots$ ( A125313), where $\gamma$ is the Euler–Mascheroni constant.

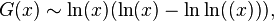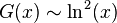In the paper <ref name=Cadwell1971">Cadwell, J. H. (1971), "Large Intervals Between Consecutive Primes", Mathematics of Computation 25 (116): 909–913, doi:10.2307/2004355 </ref> J.H. Cadwell has proposed the formula for the maximal gaps: $G(x)\sim \ln(x)(\ln(x)-\ln \ln((x))),$ which for large $x$ goes into the Cramer's conjecture $G(x)\sim \ln ^{2}(x)$ .

Thomas Nicely has calculated many large prime gaps.^[5] He measures the quality of fit to Cramér's conjecture by measuring the ratio

R={\frac {\log(p_{n})}{\sqrt {p_{n+1}-p_{n}}}}.

He writes, “For the largest known maximal gaps, $R$ has remained near 1.13.” However, 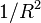$1/R^{2}$ is still less than 1, and it does not provide support to Granville's refinement that c should be greater than 1.

References

1 2 3 Cramér, Harald (1936), "On the order of magnitude of the difference between consecutive prime numbers" (PDF), Acta Arithmetica 2: 23–46
↑ Westzynthius, E. (1931), "Über die Verteilung der Zahlen die zu den n ersten Primzahlen teilerfremd sind", Commentationes Physico-Mathematicae Helsingsfors (in German) 5: 1–37, JFM 57.0186.02, Zbl 0003.24601 .
↑ Shanks, Daniel (1964), "On Maximal Gaps between Successive Primes", Mathematics of Computation (American Mathematical Society) 18 (88): 646–651, doi:10.2307/2002951, JSTOR 2002951, Zbl 0128.04203 .
↑ Granville, A. (1995), "Harald Cramér and the distribution of prime numbers" (PDF), Scandinavian Actuarial Journal 1: 12–28, doi:10.1080/03461238.1995.10413946 .
↑ Nicely, Thomas R. (1999), "New maximal prime gaps and first occurrences", Mathematics of Computation 68 (227): 1311–1315, doi:10.1090/S0025-5718-99-01065-0, MR 1627813 .

Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. A8. ISBN 978-0-387-20860-2. Zbl 1058.11001.
Pintz, János (2007). "Cramér vs. Cramér. On Cramér's probabilistic model for primes". Functiones et Approximatio Commentarii Mathematici 37: 361–376. doi:10.7169/facm/1229619660. ISSN 0208-6573. MR 2363833. Zbl 1226.11096.
Soundararajan, K. (2007). "The distribution of prime numbers". In Granville, Andrew; Rudnick, Zeév. Equidistribution in number theory, an introduction. Proceedings of the NATO Advanced Study Institute on equidistribution in number theory, Montréal, Canada, July 11--22, 2005. NATO Science Series II: Mathematics, Physics and Chemistry 237. Dordrecht: Springer-Verlag. pp. 59–83. ISBN 978-1-4020-5403-7. Zbl 1141.11043.

External links

Prime number conjectures

Hardy–Littlewood 1st 2nd Agoh–Giuga Andrica's Artin's Bateman–Horn Brocard's Bunyakovsky Chinese hypothesis Cramér's Dickson's Elliott–Halberstam Firoozbakht's Gilbreath's Grimm's Landau's problems Goldbach's weak Legendre's Twin prime Legendre's constant Lemoine's Mersenne Oppermann's Polignac's Pólya Redmond–Sun Schinzel's hypothesis H Waring's prime number

This article is issued from Wikipedia - version of the Monday, June 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.