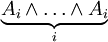Craig's theorem

In mathematical logic, Craig's theorem states that any recursively enumerable set of well-formed formulas of a first-order language is (primitively) recursively axiomatizable. This result is not related to the well-known Craig interpolation theorem, although both results are named after the same mathematician, William Craig.

Recursive axiomatization

Let 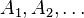$A_1,A_2,\dots$ be an enumeration of the axioms of a recursively enumerable set T of first-order formulas. Construct another set T* consisting of

\underbrace{A_i\land\dots\land A_i}_i

for each positive integer i. The deductive closures of T* and T are thus equivalent; the proof will show that T* is a decidable set. A decision procedure for T* lends itself according to the following informal reasoning. Each member of T* is either $A_1$ or of the form

\underbrace{B_j\land\dots\land B_j}_j.

Since each formula has finite length, it is checkable whether or not it is $A_1$ or of the said form. If it is of the said form and consists of j conjuncts, it is in T* if it is the expression $A_j$ ; otherwise it is not in T*. Again, it is checkable whether it is in fact $A_n$ by going through the enumeration of the axioms of T and then checking symbol-for-symbol whether the expressions are identical.

Primitive recursive axiomatizations

The proof above shows that for each recursively enumerable set of axioms there is a recursive set of axioms with the same deductive closure. A set of axioms is primitive recursive if there is a primitive recursive function that decides membership in the set. To obtain a primitive recursive aximatization, instead of replacing a formula $A_i$ with

\underbrace{A_i\land\dots\land A_i}_i

one instead replaces it with

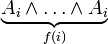\underbrace{A_i\land\dots\land A_i}_{f(i)}

(*)

where f(x) is a function that, given i, returns a computation history showing that $A_i$ is in the original recursively enumerable set of axioms. It is possible for a primitive recursive function to parse an expression of form (*) to obtain $A_i$ and j. Then, because Kleene's T predicate is primitive recursive, it is possible for a primitive recursive function to verify that j is indeed a computation history as required.

References

William Craig. On Axiomatizability Within a System, The Journal of Symbolic Logic, Vol. 18, No. 1 (1953), pp. 30-32.

This article is issued from Wikipedia - version of the Thursday, September 04, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.