Exterior covariant derivative
In mathematics, the exterior covariant derivative is an analog of an exterior derivative that takes into account the presence of a connection.
Definition
Let G be a Lie group and P → M be a principal G-bundle on a smooth manifold M. Suppose there is a connection on P so that it gives a natural direct sum decomposition of each tangent space 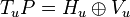 into the horizontal and vertical subspaces. Let
into the horizontal and vertical subspaces. Let 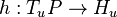 be the projection to the horizontal subspace.
be the projection to the horizontal subspace.
If ϕ is a k-form on P with values in a vector space V, then its exterior covariant derivative Dϕ is a form defined by
where vi are tangent vectors to P at u.
Suppose V is a representation of G; i.e., there is a Lie group homomorphism ρ : G → GL(V). If ϕ is equivariant in the sense:
where 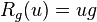 , then Dϕ is a tensorial (k + 1)-form on P of the type ρ: it is equivariant and horizontal (a form ψ is horizontal if ψ(v0, ..., vk) = ψ(hv0, ..., hvk).)
, then Dϕ is a tensorial (k + 1)-form on P of the type ρ: it is equivariant and horizontal (a form ψ is horizontal if ψ(v0, ..., vk) = ψ(hv0, ..., hvk).)
- Example: if ω is the connection form on P, then Ω = Dω is called the curvature form of ω. Bianchi's second identity says the exterior covariant derivative of Ω is zero; i.e., DΩ = 0.
We also denote the differential of ρ at the identity element by ρ:
If ϕ is a tensorial k-form of type ρ, then
where 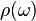 is a
is a  -valued form, and, following the notation in Lie algebra-valued differential form § Operations,
-valued form, and, following the notation in Lie algebra-valued differential form § Operations,
- Example: Bianchi's second identity (DΩ = 0) can be stated as:
![d\Omega + \operatorname{ad}(\omega) \cdot \Omega = d\Omega + [\omega \wedge \Omega] = 0](../I/m/384c228ac53cd6e62c39fe305e6d65b1.png) .
.
Unlike the usual exterior derivative, which squares to 0, we have: with F = ρ(Ω), for a tensorial zero-form ϕ,
In particular D2 vanishes for a flat connection (i.e., Ω = 0).
If ρ : G → GL(Rn), then one can write
where 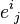 is the matrix with 1 at the (i, j)-th entry and zero on the other entries. The matrix
is the matrix with 1 at the (i, j)-th entry and zero on the other entries. The matrix 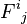 whose entries are 2-forms on P is called the curvature matrix.
whose entries are 2-forms on P is called the curvature matrix.
Exterior covariant derivative for vector bundles
When ρ : G → GL(V) is a representation, one can form the associated bundle E = P ⊗ρ V. Then the exterior covariant differentiation D given by a connection on P defines
through the correspondence between E-valued forms and tensorial forms of type ρ (see tensorial forms on principal bundles.) Requiring ∇ to satisfy Leibniz's rule, ∇ also acts on any E-valued forms. This ∇ is called the exterior covariant differentiation on E. One also sets: for a section s of E,
where 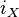 is the contraction by X. Explicitly,
is the contraction by X. Explicitly,
since 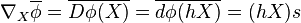 when
when 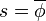 .
.
Conversely, given a vector bundle E, one can take its frame bundle, which is a principal bundle, and so gets an exterior covariant differentiation on E (depending on a connection). Identifying tensorial forms and E-valued forms, there is, for example,
![2F(X, Y) s = (-[\nabla_X, \nabla_Y] + \nabla_{[X, Y]}) s](../I/m/75e1bc780a90dcdd08d5a5e334a7b045.png) .
.
See also
Notes
- ↑ If k = 0, then, writing
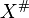 for the fundamental vector field (i.e., vertical vector field) generated by X in
for the fundamental vector field (i.e., vertical vector field) generated by X in 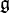 on P, we have:
on P, we have:
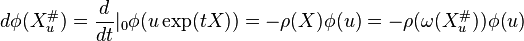 ,
,
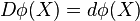 and
and 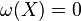 . For the general case, let Xi's be tangent vectors to P at some point such that some of Xi's are horizontal and the rest vertical. If Xi is vertical, we think of it as a Lie algebra element and then identify it with the fundamental vector field generated by it. If Xi is horizontal, we replace it with the horizontal lift of the vector field extending the pushforward πXi. This way, we have extended Xi's to vector fields. Note the extension is such that we have: [Xi, Xj] = 0 if Xi is horizontal and Xj is vertical. Finally, by the invariant formula for exterior derivative, we have:
. For the general case, let Xi's be tangent vectors to P at some point such that some of Xi's are horizontal and the rest vertical. If Xi is vertical, we think of it as a Lie algebra element and then identify it with the fundamental vector field generated by it. If Xi is horizontal, we replace it with the horizontal lift of the vector field extending the pushforward πXi. This way, we have extended Xi's to vector fields. Note the extension is such that we have: [Xi, Xj] = 0 if Xi is horizontal and Xj is vertical. Finally, by the invariant formula for exterior derivative, we have:
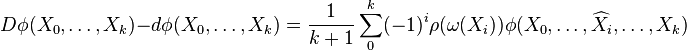 ,
,
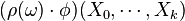 .
. - ↑ Proof: Since ρ acts on the constant part of ω, it commutes with d and thus
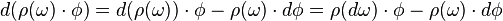 .
.
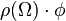 by E. Cartan's structure equation.
by E. Cartan's structure equation.
References
- Kobayashi, Shoshichi and Nomizu, Katsumi (1996). Foundations of Differential Geometry, Vol. 1 (New ed.). Wiley-Interscience. ISBN 0-471-15733-3.
| ||||||||||||||||||||||||||||||||||||||||||||||
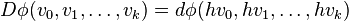
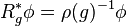
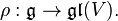
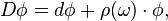
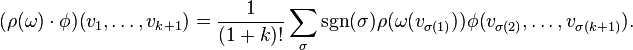
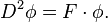
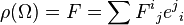
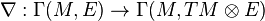
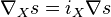
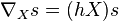
![D^2 \phi = \rho(d \omega) \cdot \phi + \rho(\omega) \cdot (\rho(\omega) \cdot \phi) = \rho(d \omega) \cdot \phi + {1 \over 2} \rho([\omega \wedge \omega]) \cdot \phi,](../I/m/17c383310e6f801ff63bba7a0a657bb0.png)