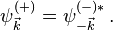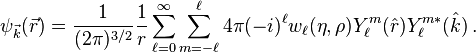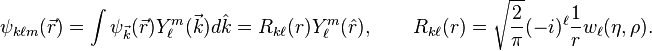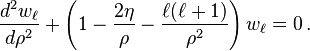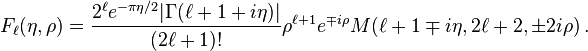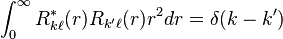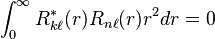Coulomb wave function

In mathematics, a Coulomb wave function is a solution of the Coulomb wave equation, named after Charles-Augustin de Coulomb. They are used to describe the behavior of charged particles in a Coulomb potential and can be written in terms of confluent hypergeometric functions or Whittaker functions of imaginary argument.

Coulomb wave equation

The Coulomb wave equation for a single charged particle is the Schrödinger equation with Coulomb potential[1]

\left(-\frac{\nabla^2}{2}+\frac{Z}{r}\right) \psi_{\vec{k}}(\vec{r}) = \frac{k^2}{2} \psi_{\vec{k}}(\vec{r}) \,,

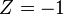where Z=Z_1 Z_2 is the product of the charges of the particle and of the field source (in units of the elementary charge, Z=-1 for hydrogen atom) and 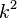k^2 is proportional to the asymptotic energy of the particle. The solution – Coulomb wave function – can be found by solving this equation in parabolic coordinates

\xi= r + \vec{r}\cdot\hat{k}, \quad \zeta= r - \vec{r}\cdot\hat{k} \qquad (\hat{k} = \vec{k}/k) \,.

Depending on the boundary conditions chosen the solution has different forms. Two of the solutions are[2]

\psi_{\vec{k}}^{(\pm)}(\vec{r}) = \frac{1}{(2\pi)^{3/2}}\Gamma(1\pm i\eta) e^{-\pi\eta/2} e^{i\vec{k}\cdot\vec{r}} M(\mp i\eta, 1, \pm ikr - i\vec{k}\cdot\vec{r}) \,,

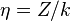where M(a,b,z) \equiv {}_1\!F_1(a;b;z) is the confluent hypergeometric function, \eta = Z/k and \Gamma(z) is the gamma function. The two boundary conditions used here are

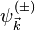\psi_{\vec{k}}^{(\pm)}(\vec{r}) \rightarrow \frac{1}{(2\pi)^{3/2}} e^{i\vec{k}\cdot\vec{r}} \qquad (\vec{r}\cdot\vec{k} \rightarrow \mp\infty) \,,

which correspond to \vec{k}-oriented plane-wave asymptotic state before or after its approach of the field source at the origin, respectively. The functions \psi_{\vec{k}}^{(\pm)} are related to each other by the formula

\psi_{\vec{k}}^{(+)} = \psi_{-\vec{k}}^{(-)*} \,.

Partial wave expansion

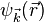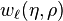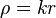The wave function \psi_{\vec{k}}(\vec{r}) can be expanded into partial waves (i.e. with respect to the angular basis) to obtain angle-independent radial functions w_\ell(\eta,\rho). Here \rho=kr.

\psi_{\vec{k}}(\vec{r}) = \frac{1}{(2\pi)^{3/2}} \frac{1}{r} \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell 4\pi(-i)^\ell w_{\ell}(\eta,\rho) Y_\ell^m (\hat{r}) Y_{\ell}^{m\ast} (\hat{k}) \,.

A single term of the expansion can be isolated by the scalar product with a specific angular state

\psi_{k\ell m}(\vec{r}) = \int \psi_{\vec{k}}(\vec{r}) Y_\ell^m (\vec{k}) d\hat{k} = R_{k\ell}(r) Y_\ell^m(\hat{r}), \qquad R_{k\ell}(r) = \sqrt{\frac{2}{\pi}} (-i)^\ell \frac{1}{r} w_\ell(\eta,\rho).

\sqrt{\frac{2}{\pi}} part seems off, wrong norm factor, orthonormality down below not true like this. Please check it. The equation for single partial wave 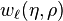w_\ell(\eta,\rho) can be obtained by rewriting the laplacian in the Coulomb wave equation in spherical coordinates and projecting the equation on a specific spherical harmonic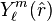 Y_\ell^m(\hat{r})

\frac{d^2 w_\ell}{d\rho^2}+\left(1-\frac{2\eta}{\rho}-\frac{\ell(\ell+1)}{\rho^2}\right)w_\ell=0 \,.

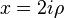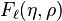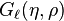The solutions are also called Coulomb (partial) wave functions. Putting x=2i\rho changes the Coulomb wave equation into the Whittaker equation, so Coulomb wave functions can be expressed in terms of Whittaker functions with imaginary arguments. Two special solutions called the regular and irregular Coulomb wave functions are denoted by F_\ell(\eta,\rho) and G_\ell(\eta,\rho), and defined in terms of the confluent hypergeometric function by[3][4]

F_\ell(\eta,\rho) = \frac{2^\ell e^{-\pi\eta/2}|\Gamma(\ell+1+i\eta)|}{(2\ell+1)!}\rho^{\ell+1}e^{\mp i\rho}M(\ell+1\mp i\eta,2\ell+2,\pm 2i\rho) \,.

The two possible sets of signs are related to each other by the Kummer transform.

Properties of the Coulomb function

The radial parts for a given angular momentum are orthonormal,[5]

\int_0^\infty R_{k\ell}^\ast(r) R_{k'\ell}(r) r^2 dr = \delta(k-k')

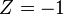and for Z=-1 they are also orthogonal to all hydrogen bound states[6]

\int_0^\infty R_{k\ell}^\ast(r) R_{n\ell}(r) r^2 dr = 0

due to being eigenstates of the same hermitian operator (the hamiltonian) with different eigenvalues.

Further reading

References

  1. ↑ Hill, Robert N. (2006), Drake, Gordon, ed., Handbook of atomic, molecular and optical physics, Springer New York, pp. 153–155
  2. ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, p. 569
  3. ↑ Thompson, I. J. (2010), "Coulomb Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
  4. ↑ Abramowitz, Milton; Stegun, Irene A., eds. (December 1972) [1964]. "Chapter 14". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 (10 ed.). New York, USA: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 538. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642.
  5. ↑ Formánek, Jiří (2004), Introduction to quantum theory I (in Czech) (2nd ed.), Prague: Academia, pp. 128–130
  6. ↑ Landau, L. D.; Lifshitz, E. M. (1977), Course of theoretical physics III: Quantum mechanics, Non-relativistic theory (3rd ed.), Pergamon Press, pp. 668–669
This article is issued from Wikipedia - version of the Wednesday, January 27, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.