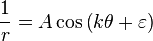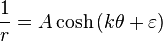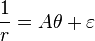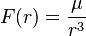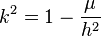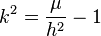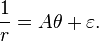Cotes's spiral

In physics and in the mathematics of plane curves, Cotes's spiral (also written Cotes' spiral and Cotes spiral) is a spiral that is typically written in one of three forms

where r and θ are the radius and azimuthal angle in a polar coordinate system, respectively, and A, k and ε are arbitrary real number constants. These spirals are named after Roger Cotes. The first form corresponds to an epispiral, and the second to one of Poinsot's spirals; the third form corresponds to a hyperbolic spiral, also known as a reciprocal spiral, which is sometimes not counted as a Cotes's spiral.^[1]

The significance of Cotes's spirals for physics is in the field of classical mechanics. These spirals are the solutions for the motion of a particle moving under an inverse-cube central force, e.g.,

where μ is any real number constant. A central force is one that depends only on the distance r between the moving particle and a point fixed in space, the center. In this case, the constant k of the spiral can be determined from μ and the areal velocity of the particle h by the formula

when μ < h ² (cosine form of the spiral) and

when μ > h ² (hyperbolic cosine form of the spiral). When μ = h ² exactly, the particle follows the third form of the spiral

See also

• Archimedean spiral
• Hyperbolic spiral
• Newton's theorem of revolving orbits
• Bertrand's theorem

References

1. ↑ Nathaniel Grossman (1996). The sheer joy of celestial mechanics. Springer. p. 34. ISBN 978-0-8176-3832-0. 

Bibliography

• Whittaker ET (1937). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies (4th ed.). New York: Dover Publications. pp. 80–83. ISBN 978-0-521-35883-5. 
• Roger Cotes (1722) Harmonia Mensuarum, pp. 31, 98.
• Isaac Newton (1687) Philosophiæ Naturalis Principia Mathematica, Book I, §2, Proposition 9.
• Danby JM (1988). "The Case ƒ(r) = μ/r ³ — Cotes' Spiral (§4.7)". Fundamentals of Celestial Mechanics (2nd ed., rev. ed.). Richmond, VA: Willmann-Bell. pp. 69–71. ISBN 978-0-943396-20-0. 
• Symon KR (1971). Mechanics (3rd ed.). Reading, MA: Addison-Wesley. p. 154. ISBN 978-0-201-07392-8. 

External links

• Weisstein, Eric W., "Cotes's spiral", MathWorld.