Core (graph theory)

This article is about graph homomorphisms. For the subgraph in which all vertices have high degree, see k-core.

In the mathematical field of graph theory, a core is a notion that describes behavior of a graph with respect to graph homomorphisms.

Definition

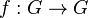Graph $G$ is a core if every homomorphism $f:G \to G$ is an isomorphism, that is it is a bijection of vertices of $G$ .

A core of a graph $H$ is a graph $G$ such that

There exists a homomorphism from $H$ to $G$ ,
there exists a homomorphism from $G$ to $H$ , and
$G$ is minimal with this property.

Two graphs are said to be homomorphism equivalent or hom-equivalent if they have isomorphic cores.

Examples

Any complete graph is a core.
A cycle of odd length is its own core.
Every two cycles of even length, and more generally every two bipartite graphs are hom-equivalent. The core of each of these graphs is the two-vertex complete graph K₂.

Properties

Every graph has a core, which is determined uniquely, up to isomorphism. The core of a graph G is always an induced subgraph of G. If $G \to H$ and $H \to G$ then the graphs $G$ and $H$ are necessarily hom-equivalent.

References

Godsil, Chris, and Royle, Gordon. Algebraic Graph Theory. Graduate Texts in Mathematics, Vol. 207. Springer-Verlag, New York, 2001. Chapter 6 section 2.
Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), "Proposition 3.5", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics 28, Heidelberg: Springer, p. 43, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058 .

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.