Coppersmith method
The Coppersmith method, proposed by Don Coppersmith, is a method to find small integer zeroes of univariate or bivariate polynomials modulo a given integer.
The method uses the Lenstra–Lenstra–Lovász lattice basis reduction algorithm (LLL) to find a polynomial that has the same zeroes as the target polynomial but smaller coefficients.[1]
In cryptography, the Coppersmith method is mainly used in attacks on RSA when parts of the secret key are known and forms a base for Coppersmith's Attack.
Approach
Coppersmith’s approach is a reduction of solving modular polynomial equations to solving polynomials over the integers.
Let 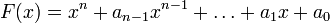 and assume that
and assume that 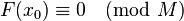 for some
integer
for some
integer 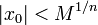 .
Coppersmith’s algorithm can be used to find this integer solution
.
Coppersmith’s algorithm can be used to find this integer solution 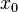 .
.
Finding roots over Q is easy using e.g. Newton's method but these algorithms do not work modulo a composite number M. The idea behind Coppersmith’s method is to find a different polynomial  related to F that has the same
related to F that has the same 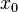 as a solution and has only small coefficients. If the coefficients and
as a solution and has only small coefficients. If the coefficients and 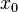 are so small that
are so small that 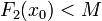 over the integers, then
over the integers, then
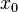 is a root of F over Q and can easily be found.
is a root of F over Q and can easily be found.
Coppersmith's algorithm uses LLL to construct the polynomial  with small coefficients.
Given F, the algorithm constructs polynomials
with small coefficients.
Given F, the algorithm constructs polynomials 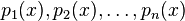 that have the same zero
that have the same zero 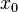 modulo
modulo 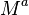 , where a is some integer chosen dependent on the degree of F and the size of
, where a is some integer chosen dependent on the degree of F and the size of 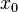 .
Any linear combination of these polynomials has zero
.
Any linear combination of these polynomials has zero 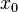 modulo
modulo 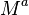 .
.
The next step is to use the LLL algorithm to construct a linear combination 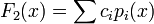 of the
of the  so that the inequality
so that the inequality 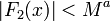 holds.
Now standard factorization methods can calculate the zeroes of
holds.
Now standard factorization methods can calculate the zeroes of 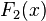 over the integers.
over the integers.
See also
References
- Bauer, A.; Joux, A. (2007). "Toward a Rigorous Variation of Coppersmith’s Algorithm on Three Variables". Lecture Notes in Computer Science 4515. Springer. pp. 361–378. doi:10.1007/978-3-540-72540-4_21.