Breusch–Pagan test

In statistics, the Breusch–Pagan test, developed in 1979 by Trevor Breusch and Adrian Pagan,[1] is used to test for heteroskedasticity in a linear regression model. It was independently suggested with some extension by R. Dennis Cook and Sanford Weisberg in 1983.[2] It tests whether the estimated variance of the residuals from a regression are dependent on the values of the independent variables. In that case, heteroskedasticity is present.

Suppose that we estimate the regression model

y = \beta_0 + \beta_1 x + u, \,

and obtain from this fitted model a set of values for 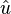\hat{u}, the residuals. Ordinary least squares constrains these so that their mean is 0 and so, given the assumption that their variance does not depend on the independent variables, an estimate of this variance can be obtained from the average of the squared values of the residuals. If the assumption is not held to be true, a simple model might be that the variance is linearly related to independent variables. Such a model can be examined by regressing the squared residuals on the independent variables, using an auxiliary regression equation of the form

\hat{u}^2 = \gamma_0 + \gamma_1 x + v.\,

This is the basis of the Breusch–Pagan test. If an F-test confirms that the independent variables are jointly significant then the null hypothesis of homoskedasticity can be rejected.

The Breusch–Pagan test tests for conditional heteroskedasticity. It is a chi-squared test: the test statistic is nχ2 with k degrees of freedom. It tests the null hypothesis of homoskedasticity. If the Chi Squared value is significant with p-value below an appropriate threshold (e.g. p<0.05) then the null hypothesis of homoskedasticity is rejected and heteroskedasticity assumed. If the Breusch–Pagan test shows that there is conditional heteroskedasticity, the original regression can be corrected by using the Hansen method, using robust standard errors, or re-thinking the regression equation by changing and/or transforming independent variables.

Procedure

Under the classical assumptions, ordinary least squares is the best linear unbiased estimator (BLUE), i.e., it is unbiased and efficient. It remains unbiased under heteroskedasticity, but efficiency is lost. Before deciding upon an estimation method, one may conduct the Breusch–Pagan test to examine the presence of heteroskedasticity. The Breusch–Pagan test is based on models of the type 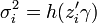\sigma_i^2 = h(z_i'\gamma) for the variances of the observations where z_i = (1, z_{2i}, \dots, z_{pi}) explain the difference in the variances. The null hypothesis is equivalent to the (p - 1)\, parameter restrictions:

\gamma_2 = \dots = \gamma_p = 0.

The following Lagrange multiplier (LM) yields the test statistic for the Breusch–Pagan test:

LM=\left (\frac{\partial l}{\partial\theta} \right )'\left (-E\left [\frac{\partial^2 l}{\partial\theta \partial\theta'} \right ] \right )^{-1}\left(\frac{\partial l}{\partial\theta} \right ).

This test is analogous to following the simple three-step procedure:[3]

y = X\beta+\varepsilon.

and compute the regression residuals.

e_i^2=\gamma_1+\gamma_2z_{2i}+\dots+\gamma_pz_{pi}+\eta_i. 
Always,z could be partly replaced by independent variables x
LM=nR^{2}\, .

The test statistic is asymptotically distributed as 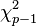\chi^2_{p - 1} under the null hypothesis of homoskedasticity.[4]

Software

In R, this test is performed by function ncvTest available in the car package,[5] or by function bptest available in the lmtest package.[6]

In Stata, one specifies the full regression, and then enters the command estat hettest followed by all independent variables.[7]

In SAS, breusch pagan can be obtained using the Proc Model option.

In Python, there is a method het_breushpagan in statsmodels.stats.diagnostic (the statsmodels package) for breusch-pagan test.

See also

References

  1. ↑ Breusch, T. S.; Pagan, A. R. (1979). "A Simple Test for Heteroskedasticity and Random Coefficient Variation". Econometrica 47 (5): 1287–1294. JSTOR 1911963. MR 545960.
  2. ↑ Cook, R. D.; Weisberg, S. (1983). "Diagnostics for Heteroskedasticity in Regression". Biometrika 70 (1): 1–10. doi:10.1093/biomet/70.1.1.
  3. ↑ Koenker, R. (1981). "A note on studentizing a test for heteroskedasticity". Journal of Econometrics 17 (1): 107–112. doi:10.1016/0304-4076(81)90062-2.
  4. ↑ Wooldridge, Jeffrey M. (2013). Introductory Econometrics: A Modern Approach (Fifth ed.). South-Western. p. 267. ISBN 978-1-111-53439-4.
  5. ↑ inside-R: ncvTest {car}
  6. ↑ R documentation about bptest
  7. ↑ "regress postestimation — Postestimation tools for regress" (PDF). Stata Manual.

Further reading

This article is issued from Wikipedia - version of the Monday, January 18, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.