Convexoid operator
In mathematics, especially operator theory, a convexoid operator is a bounded linear operator T on a complex Hilbert space H such that the closure of the numerical range coincides with the convex hull of its spectrum.
An example of such an operator is a normal operator (or some of its generalization).
A closely related operator is a spectraloid operator: an operator whose spectral radius coincides with its numerical radius. In fact, an operator T is convexoid if and only if 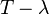 is spectraloid for every complex number
is spectraloid for every complex number  .
.
See also
- Aluthge transform
References
- T. Furuta. Certain convexoid operators
This article is issued from Wikipedia - version of the Wednesday, January 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.