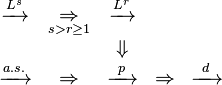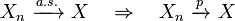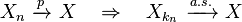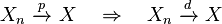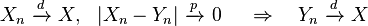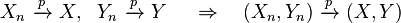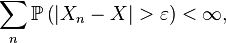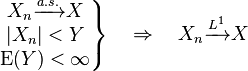Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behaviour that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behaviour can be characterised: two readily understood behaviours are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.
Background
"Stochastic convergence" formalizes the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle into a pattern. The pattern may for instance be
- Convergence in the classical sense to a fixed value, perhaps itself coming from a random event
- An increasing similarity of outcomes to what a purely deterministic function would produce
- An increasing preference towards a certain outcome
- An increasing "aversion" against straying far away from a certain outcome
Some less obvious, more theoretical patterns could be
- That the probability distribution describing the next outcome may grow increasingly similar to a certain distribution
- That the series formed by calculating the expected value of the outcome's distance from a particular value may converge to 0
- That the variance of the random variable describing the next event grows smaller and smaller.
These other types of patterns that may arise are reflected in the different types of stochastic convergence that have been studied.
While the above discussion has related to the convergence of a single series to a limiting value, the notion of the convergence of two series towards each other is also important, but this is easily handled by studying the sequence defined as either the difference or the ratio of the two series.
For example, if the average of n independent random variables Yi, i = 1, ..., n, all having the same finite mean and variance, is given by
then as n tends to infinity, Xn converges in probability (see below) to the common mean, μ, of the random variables Yi. This result is known as the weak law of large numbers. Other forms of convergence are important in other useful theorems, including the central limit theorem.
Throughout the following, we assume that (Xn) is a sequence of random variables, and X is a random variable, and all of them are defined on the same probability space  .
.
Convergence in distribution
| Dice factory | |
|---|---|
|
Suppose a new dice factory has just been built. The first few dice come out quite biased, due to imperfections in the production process. The outcome from tossing any of them will follow a distribution markedly different from the desired uniform distribution. As the factory is improved, the dice become less and less loaded, and the outcomes from tossing a newly produced die will follow the uniform distribution more and more closely. | |
| Tossing coins | |
|
Let Xn be the fraction of heads after tossing up an unbiased coin n times. Then X1 has the Bernoulli distribution with expected value μ = 0.5 and variance σ2 = 0.25. The subsequent random variables X2, X3, ... will all be distributed binomially. As n grows larger, this distribution will gradually start to take shape more and more similar to the bell curve of the normal distribution. If we shift and rescale Xn appropriately, then 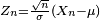 will be converging in distribution to the standard normal, the result that follows from the celebrated central limit theorem. will be converging in distribution to the standard normal, the result that follows from the celebrated central limit theorem. | |
| Graphic example | |
|
Suppose {Xi} is an iid sequence of uniform U(−1, 1) random variables. Let .gif) |
With this mode of convergence, we increasingly expect to see the next outcome in a sequence of random experiments becoming better and better modeled by a given probability distribution.
Convergence in distribution is the weakest form of convergence, since it is implied by all other types of convergence mentioned in this article. However convergence in distribution is very frequently used in practice; most often it arises from application of the central limit theorem.
Definition
A sequence X1, X2, ... of random variables is said to converge in distribution, or converge weakly, or converge in law to a random variable X if
for every number x ∈ R at which F is continuous. Here Fn and F are the cumulative distribution functions of random variables Xn and X, respectively.
The requirement that only the continuity points of F should be considered is essential. For example if Xn are distributed uniformly on intervals (0, 1/n), then this sequence converges in distribution to a degenerate random variable X = 0. Indeed, Fn(x) = 0 for all n when x ≤ 0, and Fn(x) = 1 for all x ≥ 1/n when n > 0. However, for this limiting random variable F(0) = 1, even though Fn(0) = 0 for all n. Thus the convergence of cdfs fails at the point x = 0 where F is discontinuous.
Convergence in distribution may be denoted as
where 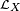 is the law (probability distribution) of X. For example if X is standard normal we can write
is the law (probability distribution) of X. For example if X is standard normal we can write 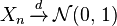 .
.
For random vectors {X1, X2, ...} ⊂ Rk the convergence in distribution is defined similarly. We say that this sequence converges in distribution to a random k-vector X if
for every A ⊂ Rk which is a continuity set of X.
The definition of convergence in distribution may be extended from random vectors to more general random elements in arbitrary metric spaces, and even to the “random variables” which are not measurable — a situation which occurs for example in the study of empirical processes. This is the “weak convergence of laws without laws being defined” — except asymptotically.[1]
In this case the term weak convergence is preferable (see weak convergence of measures), and we say that a sequence of random elements {Xn} converges weakly to X (denoted as Xn ⇒ X) if
for all continuous bounded functions h.[2] Here E* denotes the outer expectation, that is the expectation of a “smallest measurable function g that dominates h(Xn)”.
Properties
- Since F(a) = Pr(X ≤ a), the convergence in distribution means that the probability for Xn to be in a given range is approximately equal to the probability that the value of X is in that range, provided n is sufficiently large.
- In general, convergence in distribution does not imply that the sequence of corresponding probability density functions will also converge. As an example one may consider random variables with densities fn(x) = (1 − cos(2πnx))1(0,1). These random variables converge in distribution to a uniform U(0, 1), whereas their densities do not converge at all.[3]
- However, Scheffé’s lemma implies that convergence of the probability density functions implies convergence in distribution.[4]
- The portmanteau lemma provides several equivalent definitions of convergence in distribution. Although these definitions are less intuitive, they are used to prove a number of statistical theorems. The lemma states that {Xn} converges in distribution to X if and only if any of the following statements are true:
- Eƒ(Xn) → Eƒ(X) for all bounded, continuous functions ƒ (where E denotes the expected value);
- Eƒ(Xn) → Eƒ(X) for all bounded, Lipschitz functions ƒ;
- limsup{ Eƒ(Xn) } ≤ Eƒ(X) for every upper semi-continuous function ƒ bounded from above;
- liminf{ Eƒ(Xn) } ≥ Eƒ(X) for every lower semi-continuous function ƒ bounded from below;
- limsup{Pr(Xn ∈ C)} ≤ Pr(X ∈ C) for all closed sets C;
- liminf{Pr(Xn ∈ U)} ≥ Pr(X ∈ U) for all open sets U;
- lim{Pr(Xn ∈ A)} = Pr(X ∈ A) for all continuity sets A of random variable X.
- The continuous mapping theorem states that for a continuous function g, if the sequence {Xn} converges in distribution to X, then {g(Xn)} converges in distribution to g(X).
- Note however that convergence in distribution of {Xn} to X and {Yn} to Y does in general not imply convergence in distribution of {Xn + Yn} to X + Y or of {XnYn} to XY.
- Lévy’s continuity theorem: the sequence {Xn} converges in distribution to X if and only if the sequence of corresponding characteristic functions {φn} converges pointwise to the characteristic function φ of X.
- Convergence in distribution is metrizable by the Lévy–Prokhorov metric.
- A natural link to convergence in distribution is the Skorokhod's representation theorem.
Convergence in probability
| Height of a person | |
|---|---|
| This example should not be taken literally. Consider the following experiment. First, pick a random person in the street. Let X be his/her height, which is ex ante a random variable. Then you start asking other people to estimate this height by eye. Let Xn be the average of the first n responses. Then (provided there is no systematic error) by the law of large numbers, the sequence Xn will converge in probability to the random variable X. | |
| Archer | |
|
Suppose a person takes a bow and starts shooting arrows at a target. Let Xn be his score in n-th shot. Initially he will be very likely to score zeros, but as the time goes and his archery skill increases, he will become more and more likely to hit the bullseye and score 10 points. After the years of practice the probability that he hit anything but 10 will be getting increasingly smaller and smaller and will converge to 0. Thus, the sequence Xn converges in probability to X = 10. Note that Xn does not converge almost surely however. No matter how professional the archer becomes, there will always be a small probability of making an error. Thus the sequence {Xn} will never turn stationary: there will always be non-perfect scores in it, even if they are becoming increasingly less frequent. |
The basic idea behind this type of convergence is that the probability of an “unusual” outcome becomes smaller and smaller as the sequence progresses.
The concept of convergence in probability is used very often in statistics. For example, an estimator is called consistent if it converges in probability to the quantity being estimated. Convergence in probability is also the type of convergence established by the weak law of large numbers.
Definition
A sequence {Xn} of random variables converges in probability towards the random variable X if for all ε > 0
Formally, pick any ε > 0 and any δ > 0. Let Pn be the probability that Xn is outside the ball of radius ε centered at X. Then for Xn to converge in probability to X there should exist a number N (which will depend on ε and δ) such that for all n ≥ N, Pn < δ.
Convergence in probability is denoted by adding the letter p over an arrow indicating convergence, or using the “plim” probability limit operator:
For random elements {Xn} on a separable metric space (S, d), convergence in probability is defined similarly by[5]
Properties
- Convergence in probability implies convergence in distribution.[proof]
- In the opposite direction, convergence in distribution implies convergence in probability when the limiting random variable X is a constant.[proof]
- Convergence in probability does not imply almost sure convergence.[proof]
- The continuous mapping theorem states that for every continuous function g(·), if
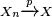 , then also
, then also 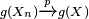 .
. - Convergence in probability defines a topology on the space of random variables over a fixed probability space. This topology is metrizable by the Ky Fan metric:[6]
or
-
![d(X,Y)=\mathbb E\left[\min(|X-Y|, 1)\right]](../I/m/7cae49ff4bbbf6f51bdecda1d712a2e8.png) .
.
Almost sure convergence
| Example 1 | |
|---|---|
| Consider an animal of some short-lived species. We record the amount of food that this animal consumes per day. This sequence of numbers will be unpredictable, but we may be quite certain that one day the number will become zero, and will stay zero forever after. | |
| Example 2 | |
|
Consider a man who tosses seven coins every morning. Each afternoon, he donates one pound to a charity for each head that appeared. The first time the result is all tails, however, he will stop permanently. Let X1, X2, … be the daily amounts the charity received from him. We may be almost sure that one day this amount will be zero, and stay zero forever after that. However, when we consider any finite number of days, there is a nonzero probability the terminating condition will not occur. |
This is the type of stochastic convergence that is most similar to pointwise convergence known from elementary real analysis.
Definition
To say that the sequence Xn converges almost surely or almost everywhere or with probability 1 or strongly towards X means that
This means that the values of Xn approach the value of X, in the sense (see almost surely) that events for which Xn does not converge to X have probability 0. Using the probability space 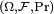 and the concept of the random variable as a function from Ω to R, this is equivalent to the statement
and the concept of the random variable as a function from Ω to R, this is equivalent to the statement
Using the notion of the limit inferior of a sequence of sets, almost sure convergence can also be defined as follows:
Almost sure convergence is often denoted by adding the letters a.s. over an arrow indicating convergence:
For generic random elements {Xn} on a metric space (S, d), convergence almost surely is defined similarly:
Properties
- Almost sure convergence implies convergence in probability (by Fatou's lemma), and hence implies convergence in distribution. It is the notion of convergence used in the strong law of large numbers.
- The concept of almost sure convergence does not come from a topology on the space of random variables. This means there is no topology on the space of random variables such that the almost surely convergent sequences are exactly the converging sequences with respect to that topology. In particular, there is no metric of almost sure convergence.
Sure convergence
To say that the sequence of random variables (Xn) defined over the same probability space (i.e., a random process) converges surely or everywhere or pointwise towards X means
where Ω is the sample space of the underlying probability space over which the random variables are defined.
This is the notion of pointwise convergence of sequence functions extended to sequence of random variables. (Note that random variables themselves are functions).
Sure convergence of a random variable implies all the other kinds of convergence stated above, but there is no payoff in probability theory by using sure convergence compared to using almost sure convergence. The difference between the two only exists on sets with probability zero. This is why the concept of sure convergence of random variables is very rarely used.
Convergence in mean
Given a real number r ≥ 1, we say that the sequence Xn converges in the r-th mean (or in the Lr-norm) towards the random variable X, if the r-th absolute moments E(|Xn|r) and E(|X|r) of Xn and X exist, and
where the operator E denotes the expected value. Convergence in r-th mean tells us that the expectation of the r-th power of the difference between Xn and X converges to zero.
This type of convergence is often denoted by adding the letter Lr over an arrow indicating convergence:
The most important cases of convergence in r-th mean are:
- When Xn converges in r-th mean to X for r = 1, we say that Xn converges in mean to X.
- When Xn converges in r-th mean to X for r = 2, we say that Xn converges in mean square to X.
Convergence in the r-th mean, for r ≥ 1, implies convergence in probability (by Markov's inequality). Furthermore, if r > s ≥ 1, convergence in r-th mean implies convergence in s-th mean. Hence, convergence in mean square implies convergence in mean.
It is also worth noticing that if 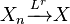 , then
, then
Properties
Provided the probability space is complete:
- If
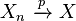 and
and 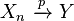 , then
, then 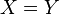 almost surely.
almost surely. - If
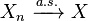 and
and 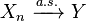 , then
, then 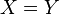 almost surely.
almost surely. - If
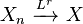 and
and 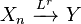 , then
, then 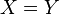 almost surely.
almost surely. - If
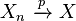 and
and 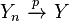 , then
, then 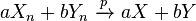 (for any real numbers
(for any real numbers  and
and  ) and
) and 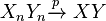 .
. - If
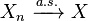 and
and 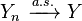 , then
, then 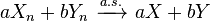 (for any real numbers
(for any real numbers  and
and  ) and
) and 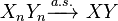 .
. - If
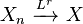 and
and 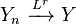 , then
, then  (for any real numbers
(for any real numbers  and
and  ).
). - None of the above statements are true for convergence in distribution.
The chain of implications between the various notions of convergence are noted in their respective sections. They are, using the arrow notation:
These properties, together with a number of other special cases, are summarized in the following list:
- Convergence in probability implies there exists a sub-sequence
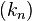 which almost surely converges:[8]
which almost surely converges:[8]
- Convergence in r-th order mean implies convergence in probability:
- Convergence in r-th order mean implies convergence in lower order mean, assuming that both orders are greater than or equal to one:
-
 provided r ≥ s ≥ 1.
provided r ≥ s ≥ 1.
-
 provided c is a constant.
provided c is a constant.
- If Xn converges in distribution to X and the difference between Xn and Yn converges in probability to zero, then Yn also converges in distribution to X:[7][proof]
- If Xn converges in distribution to X and Yn converges in distribution to a constant c, then the joint vector (Xn, Yn) converges in distribution to (X, c):[7][proof]
-
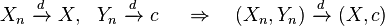 provided c is a constant.
provided c is a constant.
- Note that the condition that Yn converges to a constant is important, if it were to converge to a random variable Y then we wouldn’t be able to conclude that (Xn, Yn) converges to (X, Y).
- If Xn converges in probability to X and Yn converges in probability to Y, then the joint vector (Xn, Yn) converges in probability to (X, Y):[7][proof]
- If Xn converges in probability to X, and if P(|Xn| ≤ b) = 1 for all n and some b, then Xn converges in rth mean to X for all r ≥ 1. In other words, if Xn converges in probability to X and all random variables Xn are almost surely bounded above and below, then Xn converges to X also in any rth mean.
- Almost sure representation. Usually, convergence in distribution does not imply convergence almost surely. However for a given sequence {Xn} which converges in distribution to X0 it is always possible to find a new probability space (Ω, F, P) and random variables {Yn, n = 0, 1, ...} defined on it such that Yn is equal in distribution to Xn for each n ≥ 0, and Yn converges to Y0 almost surely.[9]
- If for all ε > 0,
- then we say that Xn converges almost completely, or almost in probability towards X. When Xn converges almost completely towards X then it also converges almost surely to X. In other words, if Xn converges in probability to X sufficiently quickly (i.e. the above sequence of tail probabilities is summable for all ε > 0), then Xn also converges almost surely to X. This is a direct implication from the Borel–Cantelli lemma.
- If Sn is a sum of n real independent random variables:
- then Sn converges almost surely if and only if Sn converges in probability.
- The dominated convergence theorem gives sufficient conditions for almost sure convergence to imply L1-convergence:
- A necessary and sufficient condition for L1 convergence is
 and the sequence (Xn) is uniformly integrable.
and the sequence (Xn) is uniformly integrable.
See also
| The Wikibook Econometric Theory has a page on the topic of: Convergence of random variables |
- Proofs of convergence of random variables
- Convergence of measures
- Continuous stochastic process: the question of continuity of a stochastic process is essentially a question of convergence, and many of the same concepts and relationships used above apply to the continuity question.
- Asymptotic distribution
- Big O in probability notation
- Skorokhod's representation theorem
- The Tweedie convergence theorem
Notes
- ↑ Bickel et al. 1998, A.8, page 475
- ↑ van der Vaart & Wellner 1996, p. 4
- ↑ Romano & Siegel 1985, Example 5.26
- ↑ Koro. "Scheffé's theorem". Archived from the original on September 15, 2015. Retrieved 1 February 2013.
- ↑ Dudley 2002, Chapter 9.2, page 287
- ↑ Dudley 2002, p. 289
- 1 2 3 4 5 6 van der Vaart 1998, Theorem 2.7
- ↑ Gut, Allan (2005). Probability: A graduate course. Theorem 3.4: Springer. ISBN 0-387-22833-0.
- ↑ van der Vaart 1998, Th.2.19
References
- Bickel, Peter J.; Klaassen, Chris A.J.; Ritov, Ya’acov; Wellner, Jon A. (1998). Efficient and adaptive estimation for semiparametric models. New York: Springer-Verlag. ISBN 0-387-98473-9.
- Billingsley, Patrick (1986). Probability and Measure. Wiley Series in Probability and Mathematical Statistics (2nd ed.). Wiley.
- Billingsley, Patrick (1999). Convergence of probability measures (2nd ed.). John Wiley & Sons. pp. 1–28. ISBN 0-471-19745-9.
- Dudley, R.M. (2002). Real analysis and probability. Cambridge, UK: Cambridge University Press. ISBN 0-521-80972-X.
- Grimmett, G.R.; Stirzaker, D.R. (1992). Probability and random processes (2nd ed.). Clarendon Press, Oxford. pp. 271–285. ISBN 0-19-853665-8.
- Jacobsen, M. (1992). Videregående Sandsynlighedsregning (Advanced Probability Theory) (3rd ed.). HCØ-tryk, Copenhagen. pp. 18–20. ISBN 87-91180-71-6.
- Ledoux, Michel; Talagrand, Michel (1991). Probability in Banach spaces. Berlin: Springer-Verlag. pp. xii+480. ISBN 3-540-52013-9. MR 1102015.
- Romano, Joseph P.; Siegel, Andrew F. (1985). Counterexamples in probability and statistics. Great Britain: Chapman & Hall. ISBN 0-412-98901-8.
- van der Vaart, Aad W.; Wellner, Jon A. (1996). Weak convergence and empirical processes. New York: Springer-Verlag. ISBN 0-387-94640-3.
- van der Vaart, Aad W. (1998). Asymptotic statistics. New York: Cambridge University Press. ISBN 978-0-521-49603-2.
- Williams, D. (1991). Probability with Martingales. Cambridge University Press. ISBN 0-521-40605-6.
- Wong, E.; Hájek, B. (1985). Stochastic Processes in Engineering Systems. New York: Springer–Verlag.
This article incorporates material from the Citizendium article "Stochastic convergence", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.
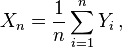
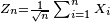 be their (normalized) sums. Then according to the
be their (normalized) sums. Then according to the 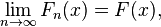
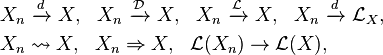
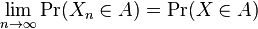
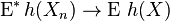
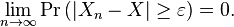
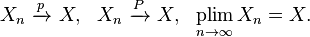
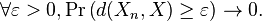

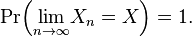
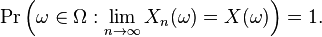
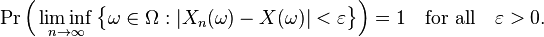
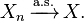
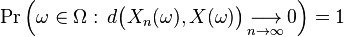

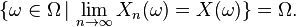
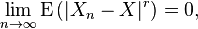
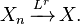
![\lim_{n \to \infty} E[|X_n|^r] = E[|X|^r]](../I/m/3b03a1eb97e99e0ef57c5464027c2c5b.png)