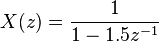Control theory

Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback. The usual objective of control theory is to control a system, often called the plant, so its output follows a desired control signal, called the reference, which may be a fixed or changing value. To do this a controller is designed, which monitors the output and compares it with the reference. The difference between actual and desired output, called the error signal, is applied as feedback to the input of the system, to bring the actual output closer to the reference. Some topics studied in control theory are stability (whether the output will converge to the reference value or oscillate about it), controllability and observability.
Extensive use is usually made of a diagrammatic style known as the block diagram. The transfer function, also known as the system function or network function, is a mathematical representation of the relation between the input and output based on the differential equations describing the system.
Although a major application of control theory is in control systems engineering, which deals with the design of process control systems for industry, other applications range far beyond this. As the general theory of feedback systems, control theory is useful wherever feedback occurs. A few examples are in physiology, electronics, climate modeling, machine design, ecosystems, navigation, neural networks, predator-prey interaction, gene expression, and production theory.[1]
Overview

Control theory is
- a theory that deals with influencing the behavior of dynamical systems
- an interdisciplinary subfield of science, which originated in engineering and mathematics, and evolved into use by the social sciences, such as economics, psychology, sociology, criminology and in the financial system.
Control systems may be thought of as having four functions: measure, compare, compute and correct. These four functions are completed by five elements: detector, transducer, transmitter, controller and final control element. The measuring function is completed by the detector, transducer and transmitter. In practical applications these three elements are typically contained in one unit. A standard example of a measuring unit is a resistance thermometer. The compare and compute functions are completed within the controller, which may be implemented electronically by proportional control, a PI controller, PID controller, bistable, hysteretic control or programmable logic controller. Older controller units have been mechanical, as in a centrifugal governor or a carburetor. The correct function is completed with a final control element. The final control element changes an input or output in the control system that affects the manipulated or controlled variable.
An example
An example of a control system is a car's cruise control, which is a device designed to maintain vehicle speed at a constant desired or reference speed provided by the driver. The controller is the cruise control, the plant is the car, and the system is the car and the cruise control. The system output is the car's speed, and the control itself is the engine's throttle position which determines how much power the engine delivers.
A primitive way to implement cruise control is simply to lock the throttle position when the driver engages cruise control. However, if the cruise control is engaged on a stretch of flat road, then the car will travel slower going uphill and faster when going downhill. This type of controller is called an open-loop controller because there is no feedback; no measurement of the system output (the car's speed) is used to alter the control (the throttle position.) As a result, the controller cannot compensate for changes acting on the car, like a change in the slope of the road.
In a closed-loop control system, data from a sensor monitoring the car's speed (the system output) enters a controller which continuously subtracts the quantity representing the speed from the reference quantity representing the desired speed. The difference, called the error, determines the throttle position (the control). The result is to match the car's speed to the reference speed (maintain the desired system output). Now, when the car goes uphill, the difference between the input (the sensed speed) and the reference continuously determines the throttle position. As the sensed speed drops below the reference, the difference increases, the throttle opens, and engine power increases, speeding up the vehicle. In this way, the controller dynamically counteracts changes to the car's speed. The central idea of these control systems is the feedback loop, the controller affects the system output, which in turn is measured and fed back to the controller.
Classification
Linear versus nonlinear control theory
The field of control theory can be divided into two branches:
- Linear control theory - This applies to systems made of devices which obey the superposition principle, which means roughly that the output is proportional to the input. They are governed by linear differential equations. A major subclass is systems which in addition have parameters which do not change with time, called linear time invariant (LTI) systems. These systems are amenable to powerful frequency domain mathematical techniques of great generality, such as the Laplace transform, Fourier transform, Z transform, Bode plot, root locus, and Nyquist stability criterion. These lead to a description of the system using terms like bandwidth, frequency response, eigenvalues, gain, resonant frequencies, poles, and zeros, which give solutions for system response and design techniques for most systems of interest.
- Nonlinear control theory - This covers a wider class of systems that do not obey the superposition principle, and applies to more real-world systems, because all real control systems are nonlinear. These systems are often governed by nonlinear differential equations. The few mathematical techniques which have been developed to handle them are more difficult and much less general, often applying only to narrow categories of systems. These include limit cycle theory, Poincaré maps, Lyapunov stability theorem, and describing functions. Nonlinear systems are often analyzed using numerical methods on computers, for example by simulating their operation using a simulation language. If only solutions near a stable point are of interest, nonlinear systems can often be linearized by approximating them by a linear system using perturbation theory, and linear techniques can be used.[2]
Frequency domain versus time domain
Mathematical techniques for analyzing and designing control systems fall into two different categories:
- Frequency domain - In this type the values of the state variables, the mathematical variables representing the system's input, output and feedback are represented as functions of frequency. The input signal and the system's transfer function are converted from time functions to functions of frequency by a transform such as the Fourier transform, Laplace transform, or Z transform. The advantage of this technique is that it results in a simplification of the mathematics; the differential equations that represent the system are replaced by algebraic equations in the frequency domain which are much simpler to solve. However, frequency domain techniques can only be used with linear systems, as mentioned above.
- Time-domain state space representation - In this type the values of the state variables are represented as functions of time. With this model the system being analyzed is represented by one or more differential equations. Since frequency domain techniques are limited to linear systems, time domain is widely used to analyze real-world nonlinear systems. Although these are more difficult to solve, modern computer simulation techniques such as simulation languages have made their analysis routine.
SISO vs MIMO
Control systems can be divided into different categories depending on the number of inputs and outputs.
- Single-input single-output (SISO) - This is the simplest and most common type, in which one output is controlled by one control signal. Examples are the cruise control example above, or an audio system, in which the control input is the input audio signal and the output is the sound waves from the speaker.
- Multiple-input multiple-output (MIMO) - These are found in more complicated systems. For example, modern large telescopes such as the Keck and MMT have mirrors composed of many separate segments each controlled by an actuator. The shape of the entire mirror is constantly adjusted by a MIMO active optics control system using input from multiple sensors at the focal plane, to compensate for changes in the mirror shape due to thermal expansion, contraction, stresses as it is rotated and distortion of the wavefront due to turbulence in the atmosphere. Complicated systems such as nuclear reactors and human cells are simulated by computer as large MIMO control systems.
History

Although control systems of various types date back to antiquity, a more formal analysis of the field began with a dynamics analysis of the centrifugal governor, conducted by the physicist James Clerk Maxwell in 1868, entitled On Governors.[3] This described and analyzed the phenomenon of self-oscillation, in which lags in the system may lead to overcompensation and unstable behavior. This generated a flurry of interest in the topic, during which Maxwell's classmate, Edward John Routh, abstracted Maxwell's results for the general class of linear systems.[4] Independently, Adolf Hurwitz analyzed system stability using differential equations in 1877, resulting in what is now known as the Routh–Hurwitz theorem.[5][6]
A notable application of dynamic control was in the area of manned flight. The Wright brothers made their first successful test flights on December 17, 1903 and were distinguished by their ability to control their flights for substantial periods (more so than the ability to produce lift from an airfoil, which was known). Continuous, reliable control of the airplane was necessary for flights lasting longer than a few seconds.
By World War II, control theory was an important part of fire-control systems, guidance systems and electronics.
Sometimes, mechanical methods are used to improve the stability of systems. For example, ship stabilizers are fins mounted beneath the waterline and emerging laterally. In contemporary vessels, they may be gyroscopically controlled active fins, which have the capacity to change their angle of attack to counteract roll caused by wind or waves acting on the ship.
The Sidewinder missile uses small control surfaces placed at the rear of the missile with spinning disks on their outer surfaces and these are known as rollerons. Airflow over the disks spins them to a high speed. If the missile starts to roll, the gyroscopic force of the disks drives the control surface into the airflow, cancelling the motion. Thus, the Sidewinder team replaced a potentially complex control system with a simple mechanical solution.
The Space Race also depended on accurate spacecraft control, and control theory has also seen an increasing use in fields such as economics.
People in systems and control
Many active and historical figures made significant contribution to control theory including:
- Pierre-Simon Laplace (1749-1827) invented the Z-transform in his work on probability theory, now used to solve discrete-time control theory problems. The Z-transform is a discrete-time equivalent of the Laplace transform which is named after him.
- Alexander Lyapunov (1857–1918) in the 1890s marks the beginning of stability theory.
- Harold S. Black (1898–1983), invented the concept of negative feedback amplifiers in 1927. He managed to develop stable negative feedback amplifiers in the 1930s.
- Harry Nyquist (1889–1976) developed the Nyquist stability criterion for feedback systems in the 1930s.
- Richard Bellman (1920–1984) developed dynamic programming since the 1940s.[7]
- Andrey Kolmogorov (1903–1987) co-developed the Wiener–Kolmogorov filter in 1941.
- Norbert Wiener (1894–1964) co-developed the Wiener–Kolmogorov filter and coined the term cybernetics in the 1940s.
- John R. Ragazzini (1912–1988) introduced digital control and the use of Z-transform in control theory (invented by Laplace) in the 1950s.
- Lev Pontryagin (1908–1988) introduced the maximum principle and the bang-bang principle.
- Pierre-Louis Lions (1956) developed viscosity solutions into stochastic control and optimal control methods.
Classical control theory
To overcome the limitations of the open-loop controller, control theory introduces feedback. A closed-loop controller uses feedback to control states or outputs of a dynamical system. Its name comes from the information path in the system: process inputs (e.g., voltage applied to an electric motor) have an effect on the process outputs (e.g., speed or torque of the motor), which is measured with sensors and processed by the controller; the result (the control signal) is "fed back" as input to the process, closing the loop.
Closed-loop controllers have the following advantages over open-loop controllers:
- disturbance rejection (such as hills in the cruise control example above)
- guaranteed performance even with model uncertainties, when the model structure does not match perfectly the real process and the model parameters are not exact
- unstable processes can be stabilized
- reduced sensitivity to parameter variations
- improved reference tracking performance
In some systems, closed-loop and open-loop control are used simultaneously. In such systems, the open-loop control is termed feedforward and serves to further improve reference tracking performance.
A common closed-loop controller architecture is the PID controller.
Closed-loop transfer function
The output of the system y(t) is fed back through a sensor measurement F to the reference value r(t). The controller C then takes the error e (difference) between the reference and the output to change the inputs u to the system under control P. This is shown in the figure. This kind of controller is a closed-loop controller or feedback controller.
This is called a single-input-single-output (SISO) control system; MIMO (i.e., Multi-Input-Multi-Output) systems, with more than one input/output, are common. In such cases variables are represented through vectors instead of simple scalar values. For some distributed parameter systems the vectors may be infinite-dimensional (typically functions).

If we assume the controller C, the plant P, and the sensor F are linear and time-invariant (i.e., elements of their transfer function C(s), P(s), and F(s) do not depend on time), the systems above can be analysed using the Laplace transform on the variables. This gives the following relations:
Solving for Y(s) in terms of R(s) gives:
The expression 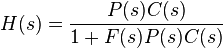 is referred to as the closed-loop transfer function of the system. The numerator is the forward (open-loop) gain from r to y, and the denominator is one plus the gain in going around the feedback loop, the so-called loop gain. If
is referred to as the closed-loop transfer function of the system. The numerator is the forward (open-loop) gain from r to y, and the denominator is one plus the gain in going around the feedback loop, the so-called loop gain. If 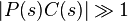 , i.e., it has a large norm with each value of s, and if
, i.e., it has a large norm with each value of s, and if 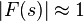 , then Y(s) is approximately equal to R(s) and the output closely tracks the reference input.
, then Y(s) is approximately equal to R(s) and the output closely tracks the reference input.
PID controller
The PID controller is probably the most-used feedback control design. PID is an initialism for Proportional-Integral-Derivative, referring to the three terms operating on the error signal to produce a control signal. If u(t) is the control signal sent to the system, y(t) is the measured output and r(t) is the desired output, and tracking error 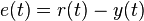 , a PID controller has the general form
, a PID controller has the general form
The desired closed loop dynamics is obtained by adjusting the three parameters 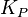 ,
, 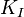 and
and 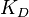 , often iteratively by "tuning" and without specific knowledge of a plant model. Stability can often be ensured using only the proportional term. The integral term permits the rejection of a step disturbance (often a striking specification in process control). The derivative term is used to provide damping or shaping of the response. PID controllers are the most well established class of control systems: however, they cannot be used in several more complicated cases, especially if MIMO systems are considered.
, often iteratively by "tuning" and without specific knowledge of a plant model. Stability can often be ensured using only the proportional term. The integral term permits the rejection of a step disturbance (often a striking specification in process control). The derivative term is used to provide damping or shaping of the response. PID controllers are the most well established class of control systems: however, they cannot be used in several more complicated cases, especially if MIMO systems are considered.
Applying Laplace transformation results in the transformed PID controller equation
with the PID controller transfer function
There exists a nice example of the closed-loop system discussed above. If we take:
PID controller transfer function in series form
1st order filter in feedback loop
linear actuator with filtered input
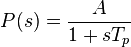 , A = const
, A = const
and insert all this into expression for closed-loop transfer function H(s), then tuning is very easy: simply put
and get H(s) = 1 identically.
For practical PID controllers, a pure differentiator is neither physically realisable nor desirable[8] due to amplification of noise and resonant modes in the system. Therefore, a phase-lead compensator type approach is used instead, or a differentiator with low-pass roll-off.
Modern control theory
In contrast to the frequency domain analysis of the classical control theory, modern control theory utilizes the time-domain state space representation, a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations. To abstract from the number of inputs, outputs and states, the variables are expressed as vectors and the differential and algebraic equations are written in matrix form (the latter only being possible when the dynamical system is linear). The state space representation (also known as the "time-domain approach") provides a convenient and compact way to model and analyze systems with multiple inputs and outputs. With inputs and outputs, we would otherwise have to write down Laplace transforms to encode all the information about a system. Unlike the frequency domain approach, the use of the state-space representation is not limited to systems with linear components and zero initial conditions. "State space" refers to the space whose axes are the state variables. The state of the system can be represented as a vector within that space.[9][10]
Topics in control theory
Stability
The stability of a general dynamical system with no input can be described with Lyapunov stability criteria.
- A linear system is called bounded-input bounded-output (BIBO) stable if its output will stay bounded for any bounded input.
- Stability for nonlinear systems that take an input is input-to-state stability (ISS), which combines Lyapunov stability and a notion similar to BIBO stability.
For simplicity, the following descriptions focus on continuous-time and discrete-time linear systems.
Mathematically, this means that for a causal linear system to be stable all of the poles of its transfer function must have negative-real values, i.e. the real part of each pole must be less than zero. Practically speaking, stability requires that the transfer function complex poles reside:
- in the open left half of the complex plane for continuous time, when the Laplace transform is used to obtain the transfer function.
- inside the unit circle for discrete time, when the Z-transform is used.
The difference between the two cases is simply due to the traditional method of plotting continuous time versus discrete time transfer functions. The continuous Laplace transform is in Cartesian coordinates where the  axis is the real axis and the discrete Z-transform is in circular coordinates where the
axis is the real axis and the discrete Z-transform is in circular coordinates where the  axis is the real axis.
axis is the real axis.
When the appropriate conditions above are satisfied a system is said to be asymptotically stable: the variables of an asymptotically stable control system always decrease from their initial value and do not show permanent oscillations. Permanent oscillations occur when a pole has a real part exactly equal to zero (in the continuous time case) or a modulus equal to one (in the discrete time case). If a simply stable system response neither decays nor grows over time, and has no oscillations, it is marginally stable: in this case the system transfer function has non-repeated poles at complex plane origin (i.e. their real and complex component is zero in the continuous time case). Oscillations are present when poles with real part equal to zero have an imaginary part not equal to zero.
If a system in question has an impulse response of
then the Z-transform (see this example), is given by
which has a pole in 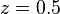 (zero imaginary part). This system is BIBO (asymptotically) stable since the pole is inside the unit circle.
(zero imaginary part). This system is BIBO (asymptotically) stable since the pole is inside the unit circle.
However, if the impulse response was
then the Z-transform is
which has a pole at 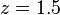 and is not BIBO stable since the pole has a modulus strictly greater than one.
and is not BIBO stable since the pole has a modulus strictly greater than one.
Numerous tools exist for the analysis of the poles of a system. These include graphical systems like the root locus, Bode plots or the Nyquist plots.
Mechanical changes can make equipment (and control systems) more stable. Sailors add ballast to improve the stability of ships. Cruise ships use antiroll fins that extend transversely from the side of the ship for perhaps 30 feet (10 m) and are continuously rotated about their axes to develop forces that oppose the roll.
Controllability and observability
Controllability and observability are main issues in the analysis of a system before deciding the best control strategy to be applied, or whether it is even possible to control or stabilize the system. Controllability is related to the possibility of forcing the system into a particular state by using an appropriate control signal. If a state is not controllable, then no signal will ever be able to control the state. If a state is not controllable, but its dynamics are stable, then the state is termed stabilizable. Observability instead is related to the possibility of observing, through output measurements, the state of a system. If a state is not observable, the controller will never be able to determine the behaviour of an unobservable state and hence cannot use it to stabilize the system. However, similar to the stabilizability condition above, if a state cannot be observed it might still be detectable.
From a geometrical point of view, looking at the states of each variable of the system to be controlled, every "bad" state of these variables must be controllable and observable to ensure a good behaviour in the closed-loop system. That is, if one of the eigenvalues of the system is not both controllable and observable, this part of the dynamics will remain untouched in the closed-loop system. If such an eigenvalue is not stable, the dynamics of this eigenvalue will be present in the closed-loop system which therefore will be unstable. Unobservable poles are not present in the transfer function realization of a state-space representation, which is why sometimes the latter is preferred in dynamical systems analysis.
Solutions to problems of uncontrollable or unobservable system include adding actuators and sensors.
Control specification
Several different control strategies have been devised in the past years. These vary from extremely general ones (PID controller), to others devoted to very particular classes of systems (especially robotics or aircraft cruise control).
A control problem can have several specifications. Stability, of course, is always present: the controller must ensure that the closed-loop system is stable, regardless of the open-loop stability. A poor choice of controller can even worsen the stability of the open-loop system, which must normally be avoided. Sometimes it would be desired to obtain particular dynamics in the closed loop: i.e. that the poles have ![Re[\lambda] < -\overline{\lambda}](../I/m/6dfab4bbfdfe60f3578a083725077ca6.png) , where
, where 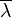 is a fixed value strictly greater than zero, instead of simply asking that
is a fixed value strictly greater than zero, instead of simply asking that ![Re[\lambda]<0](../I/m/61fcc149db100364b9694e9b3404d55a.png) .
.
Another typical specification is the rejection of a step disturbance; including an integrator in the open-loop chain (i.e. directly before the system under control) easily achieves this. Other classes of disturbances need different types of sub-systems to be included.
Other "classical" control theory specifications regard the time-response of the closed-loop system: these include the rise time (the time needed by the control system to reach the desired value after a perturbation), peak overshoot (the highest value reached by the response before reaching the desired value) and others (settling time, quarter-decay). Frequency domain specifications are usually related to robustness (see after).
Modern performance assessments use some variation of integrated tracking error (IAE,ISA,CQI).
Model identification and robustness
A control system must always have some robustness property. A robust controller is such that its properties do not change much if applied to a system slightly different from the mathematical one used for its synthesis. This specification is important: no real physical system truly behaves like the series of differential equations used to represent it mathematically. Typically a simpler mathematical model is chosen in order to simplify calculations, otherwise the true system dynamics can be so complicated that a complete model is impossible.
- System identification
The process of determining the equations that govern the model's dynamics is called system identification. This can be done off-line: for example, executing a series of measures from which to calculate an approximated mathematical model, typically its transfer function or matrix. Such identification from the output, however, cannot take account of unobservable dynamics. Sometimes the model is built directly starting from known physical equations: for example, in the case of a mass-spring-damper system we know that 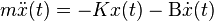 . Even assuming that a "complete" model is used in designing the controller, all the parameters included in these equations (called "nominal parameters") are never known with absolute precision; the control system will have to behave correctly even when connected to physical system with true parameter values away from nominal.
. Even assuming that a "complete" model is used in designing the controller, all the parameters included in these equations (called "nominal parameters") are never known with absolute precision; the control system will have to behave correctly even when connected to physical system with true parameter values away from nominal.
Some advanced control techniques include an "on-line" identification process (see later). The parameters of the model are calculated ("identified") while the controller itself is running: in this way, if a drastic variation of the parameters ensues (for example, if the robot's arm releases a weight), the controller will adjust itself consequently in order to ensure the correct performance.
- Analysis
Analysis of the robustness of a SISO (single input single output) control system can be performed in the frequency domain, considering the system's transfer function and using Nyquist and Bode diagrams. Topics include gain and phase margin and amplitude margin. For MIMO (multi input multi output) and, in general, more complicated control systems one must consider the theoretical results devised for each control technique (see next section): i.e., if particular robustness qualities are needed, the engineer must shift his attention to a control technique by including them in its properties.
- Constraints
A particular robustness issue is the requirement for a control system to perform properly in the presence of input and state constraints. In the physical world every signal is limited. It could happen that a controller will send control signals that cannot be followed by the physical system: for example, trying to rotate a valve at excessive speed. This can produce undesired behavior of the closed-loop system, or even damage or break actuators or other subsystems. Specific control techniques are available to solve the problem: model predictive control (see later), and anti-wind up systems. The latter consists of an additional control block that ensures that the control signal never exceeds a given threshold.
System classifications
Linear systems control
For MIMO systems, pole placement can be performed mathematically using a state space representation of the open-loop system and calculating a feedback matrix assigning poles in the desired positions. In complicated systems this can require computer-assisted calculation capabilities, and cannot always ensure robustness. Furthermore, all system states are not in general measured and so observers must be included and incorporated in pole placement design.
Nonlinear systems control
Processes in industries like robotics and the aerospace industry typically have strong nonlinear dynamics. In control theory it is sometimes possible to linearize such classes of systems and apply linear techniques, but in many cases it can be necessary to devise from scratch theories permitting control of nonlinear systems. These, e.g., feedback linearization, backstepping, sliding mode control, trajectory linearization control normally take advantage of results based on Lyapunov's theory. Differential geometry has been widely used as a tool for generalizing well-known linear control concepts to the non-linear case, as well as showing the subtleties that make it a more challenging problem. Control theory has also been used to decipher the neural mechanism that directs cognitive states.[11]
Decentralized systems control
When the system is controlled by multiple controllers, the problem is one of decentralized control. Decentralization is helpful in many ways, for instance, it helps control systems to operate over a larger geographical area. The agents in decentralized control systems can interact using communication channels and coordinate their actions.
Deterministic and stochastic systems control
A stochastic control problem is one in which the evolution of the state variables is subjected to random shocks from outside the system. A deterministic control problem is not subject to external random shocks.
Main control strategies
Every control system must guarantee first the stability of the closed-loop behavior. For linear systems, this can be obtained by directly placing the poles. Non-linear control systems use specific theories (normally based on Aleksandr Lyapunov's Theory) to ensure stability without regard to the inner dynamics of the system. The possibility to fulfill different specifications varies from the model considered and the control strategy chosen.
- List of the main control techniques
- Adaptive control uses on-line identification of the process parameters, or modification of controller gains, thereby obtaining strong robustness properties. Adaptive controls were applied for the first time in the aerospace industry in the 1950s, and have found particular success in that field.
- A hierarchical control system is a type of control system in which a set of devices and governing software is arranged in a hierarchical tree. When the links in the tree are implemented by a computer network, then that hierarchical control system is also a form of networked control system.
- Intelligent control uses various AI computing approaches like neural networks, Bayesian probability, fuzzy logic,[12] machine learning, evolutionary computation and genetic algorithms to control a dynamic system.
- Optimal control is a particular control technique in which the control signal optimizes a certain "cost index": for example, in the case of a satellite, the jet thrusts needed to bring it to desired trajectory that consume the least amount of fuel. Two optimal control design methods have been widely used in industrial applications, as it has been shown they can guarantee closed-loop stability. These are Model Predictive Control (MPC) and linear-quadratic-Gaussian control (LQG). The first can more explicitly take into account constraints on the signals in the system, which is an important feature in many industrial processes. However, the "optimal control" structure in MPC is only a means to achieve such a result, as it does not optimize a true performance index of the closed-loop control system. Together with PID controllers, MPC systems are the most widely used control technique in process control.
- Robust control deals explicitly with uncertainty in its approach to controller design. Controllers designed using robust control methods tend to be able to cope with small differences between the true system and the nominal model used for design. The early methods of Bode and others were fairly robust; the state-space methods invented in the 1960s and 1970s were sometimes found to lack robustness. Examples of modern robust control techniques include H-infinity loop-shaping developed by Duncan McFarlane and Keith Glover of Cambridge University, United Kingdom and Sliding mode control (SMC) developed by Vadim Utkin. Robust methods aim to achieve robust performance and/or stability in the presence of small modeling errors.
- Stochastic control deals with control design with uncertainty in the model. In typical stochastic control problems, it is assumed that there exist random noise and disturbances in the model and the controller, and the control design must take into account these random deviations.
- Energy-shaping control view the plant and the controller as energy-transformation devices. The control strategy is formulated in terms of interconnection (in a power-preserving manner) in order to achieve a desired behavior.
- Self-organized criticality control may be defined as attempts to interfere in the processes by which the self-organized system dissipates energy.
Applications
Optimal control theory has been applied for optimal development of oil and gas reservoirs.[13]
See also
References
- ↑ Antunes, Ricardo; Gonzalez, Vicente (3 March 2015). "A Production Model for Construction: A Theoretical Framework". Buildings 5 (1): 209–228. doi:10.3390/buildings5010209.
- ↑ trim point
- ↑ Maxwell, J.C. (1868). "On Governors". Proceedings of the Royal Society of London 16: 270–283. doi:10.1098/rspl.1867.0055. JSTOR 112510.
- ↑ Routh, E.J.; Fuller, A.T. (1975). Stability of motion. Taylor & Francis.
- ↑ Routh, E.J. (1877). A Treatise on the Stability of a Given State of Motion, Particularly Steady Motion: Particularly Steady Motion. Macmillan and co.
- ↑ Hurwitz, A. (1964). "On The Conditions Under Which An Equation Has Only Roots With Negative Real Parts". Selected Papers on Mathematical Trends in Control Theory.
- ↑ Richard Bellman (1964) Control Theory, Scientific American 211(3):186–200
- ↑ Ang, K.H., Chong, G.C.Y., and Li, Y. (2005). PID control system analysis, design, and technology, IEEE Trans Control Systems Tech, 13(4), pp.559-576.
- ↑ Donald M Wiberg. State space & linear systems. Schaum's outline series. McGraw Hill. ISBN 0-07-070096-6.
- ↑ Terrell, William (1999). "Some fundamental control theory I: Controllability, observability, and duality —AND— Some fundamental control Theory II: Feedback linearization of single input nonlinear systems". Amer. Math. Monthly 106: 705–719 and 812–828. doi:10.2307/2589614.
- ↑ Gu Shi; et al. (2015). "Controllability of structural brain networks (Article Number 8414)". Nature Communications (6). doi:10.1038/ncomms9414. Lay summary.
Here we use tools from control and network theories to offer a mechanistic explanation for how the brain moves between cognitive states drawn from the network organization of white matter microstructure.
- ↑ Liu, Jie; Wilson Wang; Farid Golnaraghi; Eric Kubica (2010). "A novel fuzzy framework for nonlinear system control". Fuzzy Sets and Systems 161 (21): 2746–2759. doi:10.1016/j.fss.2010.04.009.
- ↑ Closed-loop field development under uncertainty using optimization with sample validation. http://dx.doi.org/10.2118/173219-PA
Further reading
- Levine, William S., ed. (1996). The Control Handbook. New York: CRC Press. ISBN 978-0-8493-8570-4.
- Karl J. Åström and Richard M. Murray (2008). Feedback Systems: An Introduction for Scientists and Engineers. (PDF). Princeton University Press. ISBN 0-691-13576-2.
- Christopher Kilian (2005). Modern Control Technology. Thompson Delmar Learning. ISBN 1-4018-5806-6.
- Vannevar Bush (1929). Operational Circuit Analysis. John Wiley and Sons, Inc.
- Robert F. Stengel (1994). Optimal Control and Estimation. Dover Publications. ISBN 0-486-68200-5.
- Franklin; et al. (2002). Feedback Control of Dynamic Systems (4 ed.). New Jersey: Prentice Hall. ISBN 0-13-032393-4.
- Joseph L. Hellerstein, Dawn M. Tilbury, and Sujay Parekh (2004). Feedback Control of Computing Systems. John Wiley and Sons. ISBN 0-471-26637-X.
- Diederich Hinrichsen and Anthony J. Pritchard (2005). Mathematical Systems Theory I - Modelling, State Space Analysis, Stability and Robustness. Springer. ISBN 3-540-44125-5.
- Andrei, Neculai (2005). "Modern Control Theory - A historical Perspective" (PDF). Retrieved 2007-10-10.
- Sontag, Eduardo (1998). Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition (PDF). Springer. ISBN 0-387-98489-5.
- Goodwin, Graham (2001). Control System Design. Prentice Hall. ISBN 0-13-958653-9.
- Christophe Basso (2012). Designing Control Loops for Linear and Switching Power Supplies: A Tutorial Guide. Artech House. ISBN 978-1608075577.
- Briat, Corentin (2015). Linear Parameter-Varying and Time-Delay Systems. Analysis, Observation, Filtering & Control. Springer Verlag Heidelberg. ISBN 978-3-662-44049-0.
For Chemical Engineering
- Luyben, William (1989). Process Modeling, Simulation, and Control for Chemical Engineers. Mc Graw Hill. ISBN 0-07-039159-9.
External links
| Wikibooks has a book on the topic of: Control Systems |
| Wikimedia Commons has media related to Control theory. |
- Control Tutorials for Matlab, a set of worked-through control examples solved by several different methods.
- Control Tuning and Best Practices
- Advanced control structures, free on-line simulators explaining the control theory
- "Applying control theory to manage flash erasures/lifespan"
| ||||||||||||||||||||||||||||
| ||||||||||||||||||
|
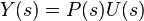
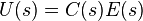
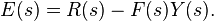
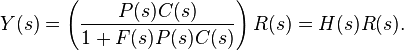
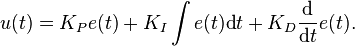
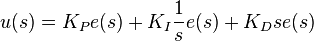
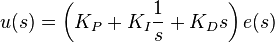
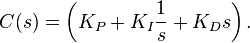
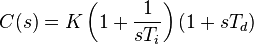
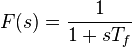
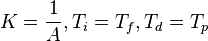
![\ x[n] = 0.5^n u[n]](../I/m/d70ec972e397b9e439e7e0cd7b7fddb0.png)
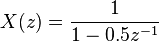
![\ x[n] = 1.5^n u[n]](../I/m/377bc70c345bab286d35625efb7834da.png)