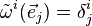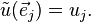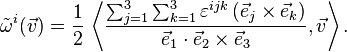Linear form

In linear algebra, a linear functional or linear form (also called a one-form or covector) is a linear map from a vector space to its field of scalars. In ℝⁿ, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the matrix product with the row vector on the left and the column vector on the right. In general, if V is a vector space over a field k, then a linear functional f is a function from V to k that is linear:

f({\vec {v}}+{\vec {w}})=f({\vec {v}})+f({\vec {w}})

for all

{\vec {v}},{\vec {w}}\in V

f(a{\vec {v}})=af({\vec {v}})

for all

{\vec {v}}\in V,a\in k.

The set of all linear functionals from V to k, Hom_k(V,k), forms a vector space over k with the addition of the operations of addition and scalar multiplication (defined pointwise). This space is called the dual space of V, or sometimes the algebraic dual space, to distinguish it from the continuous dual space. It is often written V^∗ or V′ when the field k is understood.

Continuous linear functionals

Examples and applications

Linear functionals in Rⁿ

Suppose that vectors in the real coordinate space Rⁿ are represented as column vectors

{\vec {x}}={\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}}.

Then any linear functional can be written in these coordinates as a sum of the form:

f({\vec {x}})=a_{1}x_{1}+\cdots +a_{n}x_{n}.

This is just the matrix product of the row vector [a₁ ... a_n] and the column vector ${\vec {x}}$ :

f({\vec {x}})=[a_{1}\dots a_{n}]{\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}}.

Integration

Linear functionals first appeared in functional analysis, the study of vector spaces of functions. A typical example of a linear functional is integration: the linear transformation defined by the Riemann integral

I(f)=\int _{a}^{b}f(x)\,dx

is a linear functional from the vector space C[a,b] of continuous functions on the interval [a, b] to the real numbers. The linearity of I follows from the standard facts about the integral:

I(f+g)=\int _{a}^{b}(f(x)+g(x))\,dx=\int _{a}^{b}f(x)\,dx+\int _{a}^{b}g(x)\,dx=I(f)+I(g)

I(\alpha f)=\int _{a}^{b}\alpha f(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx=\alpha I(f).

Evaluation

Let P_n denote the vector space of real-valued polynomial functions of degree ≤n defined on an interval [a,b]. If c ∈ [a, b], then let ev_c : P_n → R be the evaluation functional:

\operatorname {ev} _{c}f=f(c).

The mapping f → f(c) is linear since

(f+g)(c)=f(c)+g(c)

(\alpha f)(c)=\alpha f(c).

If x₀, ..., x_n are n+1 distinct points in [a,b], then the evaluation functionals ev_{x_i}, i=0,1,...,n form a basis of the dual space of P_n. (Lax (1996) proves this last fact using Lagrange interpolation.)

Application to quadrature

The integration functional I defined above defines a linear functional on the subspace P_n of polynomials of degree ≤ n. If x₀, …, x_n are n+1 distinct points in [a,b], then there are coefficients a₀, …, a_n for which

I(f)=a_{0}f(x_{0})+a_{1}f(x_{1})+\dots +a_{n}f(x_{n})

for all f ∈ P_n. This forms the foundation of the theory of numerical quadrature.

This follows from the fact that the linear functionals ev_{x_i} : f → f(x_i) defined above form a basis of the dual space of P_n (Lax 1996).

Linear functionals in quantum mechanics

Linear functionals are particularly important in quantum mechanics. Quantum mechanical systems are represented by Hilbert spaces, which are anti–isomorphic to their own dual spaces. A state of a quantum mechanical system can be identified with a linear functional. For more information see bra–ket notation.

Distributions

In the theory of generalized functions, certain kinds of generalized functions called distributions can be realized as linear functionals on spaces of test functions.

Properties

Any linear functional L is either trivial (equal to 0 everywhere) or surjective onto the scalar field. Indeed, this follows since just as the image of a vector subspace under a linear transformation is a subspace, so is the image of V under L. however, the only subspaces (i.e., k-subspaces) of k are {0} and k itself.

A linear functional is continuous if and only if its kernel is closed (Rudin 1991, Theorem 1.18).

Linear functionals with the same kernel are proportional.

The absolute value of any linear functional is a seminorm on its vector space.

Visualizing linear functionals

Geometric interpretation of a 1-form α as a stack of hyperplanes of constant value, each corresponding to those vectors that α maps to a given scalar value shown next to it along with the "sense" of increase. The zero plane (purple) is through the origin.

In finite dimensions, a linear functional can be visualized in terms of its level sets. In three dimensions, the level sets of a linear functional are a family of mutually parallel planes; in higher dimensions, they are parallel hyperplanes. This method of visualizing linear functionals is sometimes introduced in general relativity texts, such as Gravitation by Misner, Thorne & Wheeler (1973).

Dual vectors and bilinear forms

Linear functionals (1-forms) α, β and their sum σ and vectors u, v, w, in 3d Euclidean space. The number of (1-form) hyperplanes intersected by a vector equals the inner product.^[1]

Every non-degenerate bilinear form on a finite-dimensional vector space V gives rise to an isomorphism from V to V*. Specifically, denoting the bilinear form on V by < , > (for instance in Euclidean space <v,w> = v•w is the dot product of v and w), then there is a natural isomorphism $V\to V^{*}:v\mapsto v^{*}$ given by

v^{*}(w):=\langle v,w\rangle .

The inverse isomorphism is given by $V^{*}\to V:f\mapsto f^{*}$ where f* is the unique element of V for which for all w ∈ V

\langle f^{*},w\rangle =f(w).

The above defined vector v* ∈ V* is said to be the dual vector of v ∈ V.

In an infinite dimensional Hilbert space, analogous results hold by the Riesz representation theorem. There is a mapping V → V* into the continuous dual space V*. However, this mapping is antilinear rather than linear.

Bases in finite dimensions

Basis of the dual space in finite dimensions

Let the vector space V have a basis ${\vec {e}}_{1},{\vec {e}}_{2},\dots ,{\vec {e}}_{n}$ , not necessarily orthogonal. Then the dual space V* has a basis ${\tilde {\omega }}^{1},{\tilde {\omega }}^{2},\dots ,{\tilde {\omega }}^{n}$ called the dual basis defined by the special property that

{\tilde {\omega }}^{i}({\vec {e}}_{j})=\left\{{\begin{matrix}1&\mathrm {if} \ i=j\\0&\mathrm {if} \ i\not =j.\end{matrix}}\right.

Or, more succinctly,

{\tilde {\omega }}^{i}({\vec {e}}_{j})=\delta _{j}^{i}

where δ is the Kronecker delta. Here the superscripts of the basis functionals are not exponents but are instead contravariant indices.

A linear functional ${\tilde {u}}$ belonging to the dual space ${\tilde {V}}$ can be expressed as a linear combination of basis functionals, with coefficients ("components") u_i,

{\tilde {u}}=\sum _{i=1}^{n}u_{i}\,{\tilde {\omega }}^{i}.

Then, applying the functional ${\tilde {u}}$ to a basis vector e_j yields

{\tilde {u}}({\vec {e}}_{j})=\sum _{i=1}^{n}(u_{i}\,{\tilde {\omega }}^{i}){\vec {e}}_{j}=\sum _{i}u_{i}({\tilde {\omega }}^{i}({\vec {e}}_{j}))

due to linearity of scalar multiples of functionals and pointwise linearity of sums of functionals. Then

{\tilde {u}}({\vec {e}}_{j})=\sum _{i}u_{i}({\tilde {\omega }}^{i}({\vec {e}}_{j}))=\sum _{i}u_{i}\delta ^{i}{}_{j}=u_{j}

that is

{\tilde {u}}({\vec {e}}_{j})=u_{j}.

This last equation shows that an individual component of a linear functional can be extracted by applying the functional to a corresponding basis vector.

The dual basis and inner product

When the space V carries an inner product, then it is possible to write explicitly a formula for the dual basis of a given basis. Let V have (not necessarily orthogonal) basis ${\vec {e}}_{1},\dots ,{\vec {e}}_{n}$ . In three dimensions (n = 3), the dual basis can be written explicitly

{\tilde {\omega }}^{i}({\vec {v}})={1 \over 2}\,\left\langle {\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon ^{ijk}\,({\vec {e}}_{j}\times {\vec {e}}_{k}) \over {\vec {e}}_{1}\cdot {\vec {e}}_{2}\times {\vec {e}}_{3}},{\vec {v}}\right\rangle .

for i = 1, 2, 3, where ε is the Levi-Civita symbol and $\langle ,\rangle$ the inner product (or dot product) on V.

In higher dimensions, this generalizes as follows

{\tilde {\omega }}^{i}({\vec {v}})=\left\langle {\frac {{\underset {{}^{1\leq i_{2}<i_{3}<\dots <i_{n}\leq n}}{\sum }}\varepsilon ^{ii_{2}\dots i_{n}}(\star {\vec {e}}_{i_{2}}\wedge \dots \wedge {\vec {e}}_{i_{n}})}{\star ({\vec {e}}_{1}\wedge \dots \wedge {\vec {e}}_{n})}},{\vec {v}}\right\rangle

where $\star$ is the Hodge star operator.

References

Bishop, Richard; Goldberg, Samuel (1980), "Chapter 4", Tensor Analysis on Manifolds, Dover Publications, ISBN 0-486-64039-6
Halmos, Paul (1974), Finite dimensional vector spaces, Springer, ISBN 0-387-90093-4
Lax, Peter (1996), Linear algebra, Wiley-Interscience, ISBN 978-0-471-11111-5
Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0
Rudin, Walter (1991), Functional Analysis, McGraw-Hill Science/Engineering/Math, ISBN 978-0-07-054236-5
Schutz, Bernard (1985), "Chapter 3", A first course in general relativity, Cambridge, UK: Cambridge University Press, ISBN 0-521-27703-5

↑ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 57. ISBN 0-7167-0344-0.

Functional analysis

Set / subset types	Absolutely convex Absorbing Balanced Bounded Convex Radial Star-shaped Symmetric Linear cone (subset) Convex cone (subset)

TVS types	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Webbed Topological tensor product (of Hilbert spaces)

Mapping topologies	Dual Dual space Operator Strong (polar operator) Ultrastrong Weak (operator) Ultraweak Uniform convergence

Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Set operations	Algebraic interior (core) Interior Minkowski addition Polar

Banach algebras	C-algebras Spectrum (C-algebra radius) Spectral theory

Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia - version of the Tuesday, October 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.