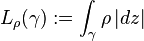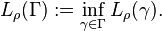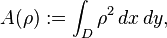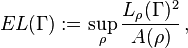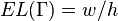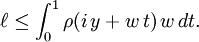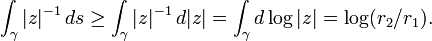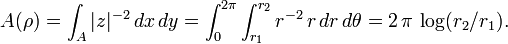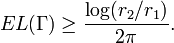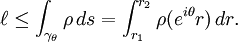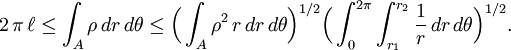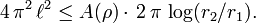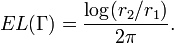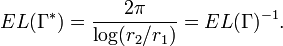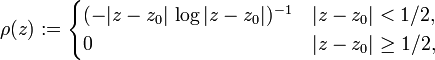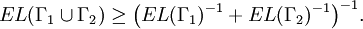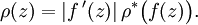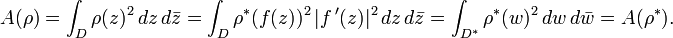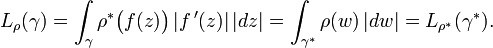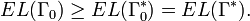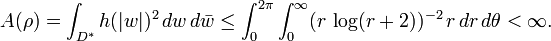Extremal length
In the mathematical theory of conformal and quasiconformal mappings, the extremal length of a collection of curves  is a measure of the size of
is a measure of the size of  that is invariant under conformal mappings. More specifically, suppose that
that is invariant under conformal mappings. More specifically, suppose that  is an open set in the complex plane and
is an open set in the complex plane and  is a collection
of paths in
is a collection
of paths in  and
and 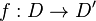 is a conformal mapping. Then the extremal length of
is a conformal mapping. Then the extremal length of  is equal to the extremal length of the image of
is equal to the extremal length of the image of  under
under  . One also works with the conformal modulus of
. One also works with the conformal modulus of  , the reciprocal of the extremal length. The fact that extremal length and conformal modulus are conformal invariants of
, the reciprocal of the extremal length. The fact that extremal length and conformal modulus are conformal invariants of  makes them useful tools in the study of conformal and quasi-conformal mappings. One also works with extremal length in dimensions greater than two and certain other metric spaces, but the following deals primarily with the two dimensional setting.
makes them useful tools in the study of conformal and quasi-conformal mappings. One also works with extremal length in dimensions greater than two and certain other metric spaces, but the following deals primarily with the two dimensional setting.
Definition of extremal length
To define extremal length, we need to first introduce several related quantities.
Let  be an open set in the complex plane. Suppose that
be an open set in the complex plane. Suppose that  is a
collection of rectifiable curves in
is a
collection of rectifiable curves in  . If
. If ![\rho:D\to [0,\infty]](../I/m/6a1ad854789b7f4e39dd8702fb76951c.png) is Borel-measurable, then for any rectifiable curve
is Borel-measurable, then for any rectifiable curve  we let
we let
denote the  –length of
–length of  , where
, where 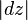 denotes the
Euclidean element of length. (It is possible that
denotes the
Euclidean element of length. (It is possible that 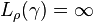 .)
What does this really mean?
If
.)
What does this really mean?
If 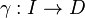 is parameterized in some interval
is parameterized in some interval  ,
then
,
then 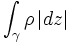 is the integral of the Borel-measurable function
is the integral of the Borel-measurable function
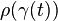 with respect to the Borel measure on
with respect to the Borel measure on  for which the measure of every subinterval
for which the measure of every subinterval 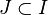 is the length of the
restriction of
is the length of the
restriction of  to
to 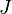 . In other words, it is the
Lebesgue-Stieltjes integral
. In other words, it is the
Lebesgue-Stieltjes integral
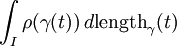 , where
, where
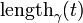 is the length of the restriction of
is the length of the restriction of  to
to 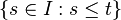 .
Also set
.
Also set
The area of  is defined as
is defined as
and the extremal length of  is
is
where the supremum is over all Borel-measureable ![\rho:D\to[0,\infty]](../I/m/6a1ad854789b7f4e39dd8702fb76951c.png) with
with 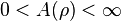 . If
. If  contains some non-rectifiable curves and
contains some non-rectifiable curves and
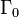 denotes the set of rectifiable curves in
denotes the set of rectifiable curves in  , then
, then
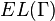 is defined to be
is defined to be 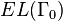 .
.
The term (conformal) modulus of  refers to
refers to 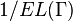 .
.
The extremal distance in  between two sets in
between two sets in 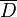 is the extremal length of the collection of curves in
is the extremal length of the collection of curves in  with one endpoint in one set and the other endpoint in the other set.
with one endpoint in one set and the other endpoint in the other set.
Examples
In this section the extremal length is calculated in several examples. The first three of these examples are actually useful in applications of extremal length.
Extremal distance in rectangle
Fix some positive numbers 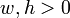 , and let
, and let  be the rectangle
be the rectangle
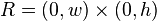 . Let
. Let  be the set of all finite
length curves
be the set of all finite
length curves 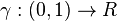 that cross the rectangle left to right,
in the sense that
that cross the rectangle left to right,
in the sense that 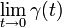 is on the left edge
is on the left edge ![\{0\}\times[0,h]](../I/m/aae0508572ad7f8e268afaa3c16c15c7.png) of the rectangle, and
of the rectangle, and
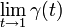 is on the right edge
is on the right edge ![\{1\}\times[0,h]](../I/m/aa94cac2c8452cb8a6464321e7bb2f97.png) .
(The limits necessarily exist, because we are assuming that
.
(The limits necessarily exist, because we are assuming that  has finite length.) We will now prove that in this case
has finite length.) We will now prove that in this case
First, we may take 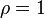 on
on  . This
. This  gives
gives 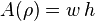 and
and 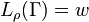 . The definition
of
. The definition
of 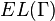 as a supremum then gives
as a supremum then gives 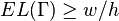 .
.
The opposite inequality is not quite so easy. Consider an arbitrary
Borel-measurable ![\rho:R\to[0,\infty]](../I/m/db94eb059d493f3e495ebaf09fa81685.png) such that
such that
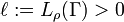 .
For
.
For 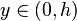 , let
, let 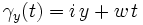 (where we are identifying
(where we are identifying 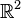 with the complex plane).
Then
with the complex plane).
Then 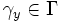 , and hence
, and hence 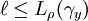 .
The latter inequality may be written as
.
The latter inequality may be written as
Integrating this inequality over 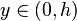 implies
implies
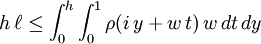 .
.
Now a change of variable 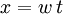 and an application of the Cauchy-Schwarz inequality give
and an application of the Cauchy-Schwarz inequality give
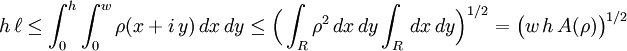 . This gives
. This gives 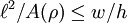 .
.
Therefore, 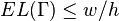 , as required.
, as required.
As the proof shows, the extremal length of  is the same as the extremal
length of the much smaller collection of curves
is the same as the extremal
length of the much smaller collection of curves 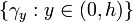 .
.
It should be pointed out that the extremal length of the family of curves 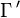 that connect the bottom edge of
that connect the bottom edge of  to the top edge of
to the top edge of  satisfies
satisfies
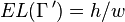 , by the same argument. Therefore,
, by the same argument. Therefore, 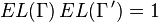 .
It is natural to refer to this as a duality property of extremal length, and a similar duality property
occurs in the context of the next subsection. Observe that obtaining a lower bound on
.
It is natural to refer to this as a duality property of extremal length, and a similar duality property
occurs in the context of the next subsection. Observe that obtaining a lower bound on
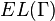 is generally easier than obtaining an upper bound, since the lower bound involves
choosing a reasonably good
is generally easier than obtaining an upper bound, since the lower bound involves
choosing a reasonably good  and estimating
and estimating 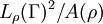 ,
while the upper bound involves proving a statement about all possible
,
while the upper bound involves proving a statement about all possible  . For this reason,
duality is often useful when it can be established: when we know that
. For this reason,
duality is often useful when it can be established: when we know that 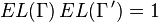 ,
a lower bound on
,
a lower bound on 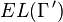 translates to an upper bound on
translates to an upper bound on 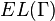 .
.
Extremal distance in annulus
Let 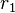 and
and  be two radii satisfying
be two radii satisfying
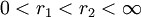 . Let
. Let  be the
annulus
be the
annulus 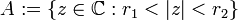 and let
and let
 and
and  be the two boundary components
of
be the two boundary components
of  :
: 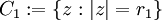 and
and 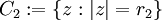 . Consider the extremal distance
in
. Consider the extremal distance
in  between
between  and
and  ;
which is the extremal length of the collection
;
which is the extremal length of the collection  of
curves
of
curves 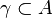 connecting
connecting  and
and  .
.
To obtain a lower bound on 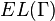 ,
we take
,
we take 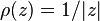 . Then for
. Then for 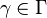 oriented from
oriented from  to
to 
On the other hand,
We conclude that
We now see that this inequality is really an equality by employing an argument similar to the one given above for the rectangle. Consider an arbitrary Borel-measurable  such that
such that 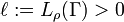 . For
. For 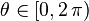 let
let 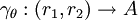 denote the curve
denote the curve 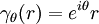 . Then
. Then
We integrate over  and apply the Cauchy-Schwarz inequality, to obtain:
and apply the Cauchy-Schwarz inequality, to obtain:
Squaring gives
This implies the upper bound 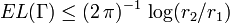 .
When combined with the lower bound, this yields the exact value of the extremal length:
.
When combined with the lower bound, this yields the exact value of the extremal length:
Extremal length around an annulus
Let 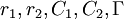 and
and  be as above, but now let
be as above, but now let 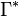 be the collection of all curves that wind once around the annulus, separating
be the collection of all curves that wind once around the annulus, separating  from
from  . Using the above methods, it is not hard to show that
. Using the above methods, it is not hard to show that
This illustrates another instance of extremal length duality.
Extremal length of topologically essential paths in projective plane
In the above examples, the extremal  which maximized the
ratio
which maximized the
ratio 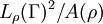 and gave the extremal length corresponded to a flat metric. In other words, when the Euclidean Riemannian metric of the corresponding planar domain is scaled by
and gave the extremal length corresponded to a flat metric. In other words, when the Euclidean Riemannian metric of the corresponding planar domain is scaled by  , the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinder. We now discuss an example where an extremal metric is not flat. The projective plane with the spherical metric is obtained by identifying antipodal points on the unit sphere in
, the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinder. We now discuss an example where an extremal metric is not flat. The projective plane with the spherical metric is obtained by identifying antipodal points on the unit sphere in 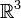 with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map
with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map 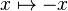 . Let
. Let  denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in
denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in  is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family.[1] (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is
is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family.[1] (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is 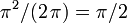 .
.
Extremal length of paths containing a point
If  is any collection of paths all of which have positive diameter and containing a point
is any collection of paths all of which have positive diameter and containing a point 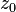 , then
, then 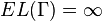 . This follows, for example, by taking
. This follows, for example, by taking
which satisfies 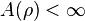 and
and 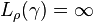 for every rectifiable
for every rectifiable 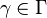 .
.
Elementary properties of extremal length
The extremal length satisfies a few simple monotonicity properties. First, it is clear that if 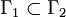 , then
, then 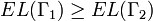 .
Moreover, the same conclusion holds if every curve
.
Moreover, the same conclusion holds if every curve 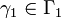 contains a curve
contains a curve 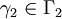 as a subcurve (that is,
as a subcurve (that is,  is the restriction of
is the restriction of  to a subinterval of its domain). Another sometimes useful inequality is
to a subinterval of its domain). Another sometimes useful inequality is
This is clear if 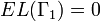 or if
or if 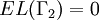 , in which case the right hand side is interpreted as
, in which case the right hand side is interpreted as  . So suppose that this is not the case and with no loss of generality assume that the curves in
. So suppose that this is not the case and with no loss of generality assume that the curves in 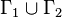 are all rectifiable. Let
are all rectifiable. Let 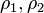 satisfy
satisfy 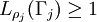 for
for 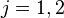 . Set
. Set 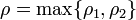 . Then
. Then 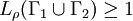 and
and 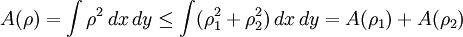 , which proves the inequality.
, which proves the inequality.
Conformal invariance of extremal length
Let 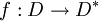 be a conformal homeomorphism
(a bijective holomorphic map) between planar domains. Suppose that
be a conformal homeomorphism
(a bijective holomorphic map) between planar domains. Suppose that
 is a collection of curves in
is a collection of curves in  ,
and let
,
and let 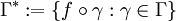 denote the
image curves under
denote the
image curves under  . Then
. Then 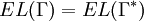 .
This conformal invariance statement is the primary reason why the concept of
extremal length is useful.
.
This conformal invariance statement is the primary reason why the concept of
extremal length is useful.
Here is a proof of conformal invariance. Let 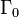 denote the set of curves
denote the set of curves
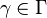 such that
such that  is rectifiable, and let
is rectifiable, and let
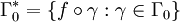 , which is the set of rectifiable
curves in
, which is the set of rectifiable
curves in 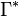 . Suppose that
. Suppose that ![\rho^*:D^*\to[0,\infty]](../I/m/ad82f17e8369cf12983d2ee2a0a3ebb8.png) is Borel-measurable. Define
is Borel-measurable. Define
A change of variables 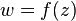 gives
gives
Now suppose that 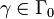 is rectifiable, and set
is rectifiable, and set 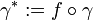 . Formally, we may use a change of variables again:
. Formally, we may use a change of variables again:
To justify this formal calculation, suppose that  is defined in some interval
is defined in some interval  , let
, let
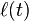 denote the length of the restriction of
denote the length of the restriction of  to
to ![I\cap(-\infty,t]](../I/m/1ad52f80f3628fc98663ead71204ee04.png) ,
and let
,
and let 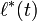 be similarly defined with
be similarly defined with  in place of
in place of  . Then it is easy to see that
. Then it is easy to see that 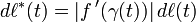 , and this implies
, and this implies 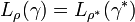 , as required. The above equalities give,
, as required. The above equalities give,
If we knew that each curve in  and
and 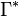 was rectifiable, this would
prove
was rectifiable, this would
prove 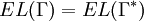 since we may also apply the above with
since we may also apply the above with  replaced by its inverse
and
replaced by its inverse
and  interchanged with
interchanged with 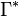 . It remains to handle the non-rectifiable curves.
. It remains to handle the non-rectifiable curves.
Now let 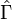 denote the set of rectifiable curves
denote the set of rectifiable curves 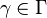 such that
such that  is
non-rectifiable. We claim that
is
non-rectifiable. We claim that 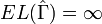 .
Indeed, take
.
Indeed, take 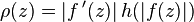 , where
, where 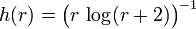 .
Then a change of variable as above gives
.
Then a change of variable as above gives
For 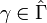 and
and 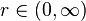 such that
such that  is contained in
is contained in 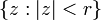 , we have
, we have
![L_\rho(\gamma)\ge\inf\{h(s):s\in[0,r]\}\,\mathrm{length}(f\circ\gamma)=\infty](../I/m/fb9d2e148a4fd77c08d1d4a5d1387348.png) .
.
On the other hand, suppose that 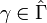 is such that
is such that  is unbounded.
Set
is unbounded.
Set 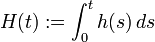 . Then
. Then
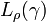 is at least the length of the curve
is at least the length of the curve 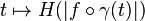 (from an interval in
(from an interval in 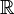 to
to 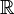 ). Since
). Since 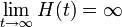 ,
it follows that
,
it follows that 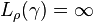 .
Thus, indeed,
.
Thus, indeed, 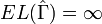 .
.
Using the results of the previous section, we have
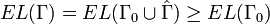 .
.
We have already seen that 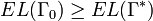 . Thus,
. Thus, 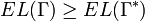 .
The reverse inequality holds by symmetry, and conformal invariance is therefore established.
.
The reverse inequality holds by symmetry, and conformal invariance is therefore established.
Some applications of extremal length
By the calculation of the extremal distance in an annulus and the conformal
invariance it follows that the annulus 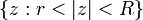 (where
(where 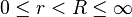 )
is not conformally homeomorphic to the annulus
)
is not conformally homeomorphic to the annulus 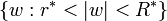 if
if 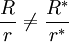 .
.
Extremal length in higher dimensions
The notion of extremal length adapts to the study of various problems in dimensions 3 and higher, especially in relation to quasiconformal mappings.
Discrete extremal length
Suppose that  is some graph and
is some graph and  is a collection of paths in
is a collection of paths in  . There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin,[2] consider a function
. There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin,[2] consider a function 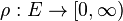 . The
. The  -length of a path is defined as the sum of
-length of a path is defined as the sum of 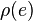 over all edges in the path, counted with multiplicity. The "area"
over all edges in the path, counted with multiplicity. The "area" 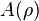 is defined as
is defined as 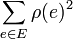 . The extremal length of
. The extremal length of  is then defined as before. If
is then defined as before. If  is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theory.
is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theory.
Another notion of discrete extremal length that is appropriate in other contexts is vertex extremal length, where 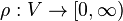 , the area is
, the area is 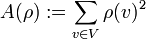 , and the length of a path is the sum of
, and the length of a path is the sum of 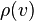 over the vertices visited by the path, with multiplicity.
over the vertices visited by the path, with multiplicity.
Notes
References
- Ahlfors, Lars V. (1973), Conformal invariants: topics in geometric function theory, New York: McGraw-Hill Book Co., MR 0357743
- Duffin, R. J. (1962), "The extremal length of a network", Journal of Mathematical Analysis and Applications 5 (2): 200–215, doi:10.1016/S0022-247X(62)80004-3
- Lehto, O.; Virtanen, K. I. (1973), Quasiconformal mappings in the plane (2nd ed.), Berlin, New York: Springer-Verlag